Języki skryptowe - Python¶

Wykład 5¶

timeit, czyli pythonowy stoper
złożoność algorytmów + przykłady
notacja "dużego Ο" (Omicron)
algorytmy sortowania

Dygresja o main¶

import math

print(__name__)      # nazwa skryptu
print(math.__name__) # nazwa zaimportowanego modułu

__main__
math

# instrukcje z main
# z zaimportowanych modułów
# nie zostaną wywołane

if __name__ == "__main__":
    print("Hello World!")

Hello World!

timeit¶

def silnia(n):
    """Zwraca silnię liczby n."""
    if n < 2:
        return 1 # 0! = 1, 1! = 1
    return n*silnia(n - 1)

from timeit import timeit

# timeit(funkcja, setup, number) -> czas wykonania funkcji w s
# funkcja - funkcja do wykonania
# setup - konfiguracja
# number - liczba powtórzeń
timeit("silnia(10)", setup="from __main__ import silnia", number=10)

3.7365999560279306e-05

timeit("silnia(100)", setup="from __main__ import silnia", number=10)

0.0004746449994854629

timeit z linii komend¶

# silnia.py

def silnia(n):
    """Zwraca silnię liczby n."""
    if n < 2:
        return 1 # 0! = 1, 1! = 1
    return n*silnia(n - 1)

możemy przetestować naszą funkcję z linii komend

$ python -m timeit -n10 'from silnia import silnia; silnia(10)'
10 loops, best of 3: 9.11 usec per loop

timeit w Jupyter Notebook¶

def silnia(n):
    """Zwraca silnię liczby n."""
    if n < 2:
        return 1 # 0! = 1, 1! = 1
    return n*silnia(n - 1)

%timeit -n10 silnia(10)

10 loops, best of 3: 3.44 µs per loop

Algorytm - ciąg instrukcji prowadzących do rozwiązania zadania

Algorytm: egzamin

Koty Ali¶

Pierwszego dnia Ala dostała jednego kota. Każdego kolejnego dnia dostaje o jednego więcej niż dnia poprzedniego. Ile kotów ma Ala po n dniach?
- pierwszy dzień: 1
- drugi dzień: 1 + 1
- trzeci dzień: 1 + 1 + 1 ...

Koty Ali - algorytm I¶

def licz_koty_v1(n):
    """Zwraca liczbę kotów po n dniach."""
    n_cats = 0                     # Ala nie ma kota
    for dzien in range(1, n + 1):  # pętla po dniach
        for koty in range(dzien):  # liczba kotów = nr dnia
            n_cats += 1            # dodaj kota
    return n_cats                  # dwie pętle -> n*n operacji

%timeit -n3 licz_koty_v1(10000) # liczba kotów po 10 dniach

3 loops, best of 3: 4.43 s per loop

Koty Ali - algorytm II¶

def licz_koty_v2(n):
    """Zwraca liczbę kotów po n dniach."""
    n_cats = 0                     # Ala nie ma kota
    for dzien in range(1, n + 1):  # pętla po dniach
        n_cats += dzien            # dodaj koty (= nr dnia)
    return n_cats                  # jedna pętla -> n operacji

%timeit -n3 licz_koty_v2(10000) # liczba kotów po 10 dniach

3 loops, best of 3: 904 µs per loop

Koty Ali - algorytm III¶

def licz_koty_v3(n):
    """Zwraca liczbę kotów po n dniach."""
    return n * (n + 1) // 2 # jedna operacja

%timeit -n3 licz_koty_v3(10000) # liczba kotów po 10 dniach

3 loops, best of 3: 535 ns per loop

Koty Ali - algorytm IV¶

def licz_koty_v4(n):
    """Zwraca liczbę kotów po n dniach."""
    koty = list(range(n + 1)) # n zmiennych w pamięci
    return sum(koty)          # jedna pętla -> n operacji

%timeit -n3 licz_koty_v4(10000) # liczba kotów po 10 dniach

3 loops, best of 3: 411 µs per loop

range vs list(range)¶

$ python -m timeit -n10 'range(1000000)'
10 loops, best of 3: 0.684 usec per loop

$ python -m timeit -n10 'list(range(1000000))'
10 loops, best of 3: 52.3 msec per loop

Koty Ali - algorytm V¶

def licz_koty_v5(n):
    """Zwraca liczbę kotów po n dniach."""
    return sum(range(n + 1)) # jedna pętla -> n operacji

%timeit -n3 licz_koty_v5(10000) # liczba kotów po 10 dniach

3 loops, best of 3: 471 µs per loop

Złożoność algorytmu¶

złożoność czasowa -> liczba operacji
złożoność pamięciowa -> ilość potrzebnej pamięci

	Alg I	Alg II	Alg III	Alg IV	Alg V
operacje	$n^2$	$n$	$1$	$n$	n
pamięć	$1$	$1$	$1$	$n$	1
czas	4.6 s	973 $\mu$s	768 ns	661 $\mu$s	475 $\mu$s

Wartość wielomianu¶

Dany jest wielomian:

\[ W(x) = a_0 + a_1\cdot x + a_2 \cdot x^2 + ... + a_n \cdot x^n\]

Korzystając bezpośrednio z powyższgo wzoru należy wykonać $n$ dodawań oraz $1 + 2 + ... + n = \frac{n\cdot(n+1)}{2}$ mnożeń

Metoda naiwna¶

def naive(a, x):
    """Zwraca wartość wielomianu o współczynnikach a w punkcie x."""
    result = 0
    for i, ai in enumerate(a): # i - indeks, ai - współczynnik a_i
        result += ai * x**i    # W(x) += a_i * x^i
    return result

a = range(500)
x = 3.5

naive(a, x)

2.1569220024001972e+274

%timeit -n3 naive(a, x)

3 loops, best of 3: 259 µs per loop

Schemat Hornera¶

Zapisując wielomian w postaci:

\[W(x) = a_0 + x\cdot(a_1 + x\cdot(a_2 + ... + x\cdot(a_{n-1} + a_n\cdot x)...)\]

organiczamy się do $n$ dodań i $n$ mnożeń

Algorytm Hornera¶

\[W(x) = a_0 + x\cdot(a_1 + x\cdot(a_2 + ... + x\cdot(a_{n-1} + a_n\cdot x)...)\]

Niech

\[b_n = a_n$$ $$b_{n-1} = b_n\cdot x + a_{n-1}$$ $$b_{n-2} = n_{n-1}\cdot x + a_{n-2}$$ $$...$$ $$b_1 = b_2\cdot x + a_1$$ $$b_0 = b_1\cdot x + a_0\]

$b_0$ - wartość wielomianu

Horner vs Naive¶

def horner(a, x):
    """Zwraca wartość wielomianu o współczynnikach a w punkcie x."""
    result = 0
    for w in a[-1::-1]:         # "reverse"
        result = result * x + w # b_i = b_{i-1} * x + a_i
    return result

a = range(500)
x = 3.5

horner(a, x)

2.156922002400198e+274

%timeit -n3 horner(a, x)

3 loops, best of 3: 98.1 µs per loop

%timeit -n3 naive(a, x)

3 loops, best of 3: 257 µs per loop

Złożoność algorytmów¶

czas w zależności od rozmiaru danych (N)
zajęta pamięć (pomijając dane wejściowe)
najczęściej interesuje nas złożoność asymptotyczna (dla dużych N)
np. które człony $\(f(n) = n^3 +10\cdot n^2 + 100\cdot n + 1000\cdot\ln(n)$\) są znaczące?

Wkłady od różnych członów¶

def terms(f):
    """Zwraca kolejne człony funkcji f (oddzielone +)."""    
    return [term.strip() for term in f.split('+')]

terms("n**2 + 10*n")

['n**2', '10*n']

def eval_f(f, n = 1):
    """Zwraca wartość funkcji f w punkcie n."""
    return eval(f)

eval_f("n**2 + 10*n", n = 5)

Wkłady od różnych członów¶

def eval_terms(*terms, n = 1):
    """Zwraca wartości kolejnych członów w punkcie n."""
    return [eval_f(term, n) for term in terms]

eval_f("n**2", n = 5), eval_f("10*n", n = 5)

(25, 50)

eval_terms(*terms("n**2 + 10*n"), n = 5)

[25, 50]

Wkłady od różnych członów¶

def print_cell(cell, width=10):
    """Drukuje pojedynczą komórkę w tabeli."""
    print(str(cell).rjust(width), end=' |')

def table_head(f, width=10):
    """Drukuje pierwsze rząd tabeli."""
    print_cell("n", width)
    for term in terms(f):
        print_cell(term, width)
    print("\n" + "-" * width * (len(terms(f)) + 2))

table_head("n**2 + 10*n")

         n |      n**2 |      10*n |
----------------------------------------

Wkłady od różnych członów¶

def f_as_table(f, *args, width=10):
    """Drukuje tabelę z procentowym wkładem każdego członu."""
    table_head(f, width)
    for n in args:
        print_cell(n, width)
        f_val = eval_f(f, n)
        for term in eval_terms(*terms(f), n = n):
            print_cell(round(term / f_val * 100), width)
        print()

f_as_table("n**2 + 10*n", 1, 10, 100, width=5)

    n | n**2 | 10*n |
--------------------
    1 |    9 |   91 |
   10 |   50 |   50 |
  100 |   91 |    9 |

Wkłady od różnych członów¶

\[f(n) = n^3 +10\cdot n^2 + 100\cdot n + 1000\cdot\ln(n)\]

from math import log

n = [10**i for i in range(5)]
f_as_table("n**3 + 10*n**2 + 100*n + 1000*log(n)", *n, width=12)

           n |        n**3 |     10*n**2 |       100*n | 1000*log(n) |
------------------------------------------------------------------------
           1 |           1 |           9 |          90 |           0 |
          10 |          19 |          19 |          19 |          43 |
         100 |          90 |           9 |           1 |           0 |
        1000 |          99 |           1 |           0 |           0 |
       10000 |         100 |           0 |           0 |           0 |

Notacja dużego Ο¶

Funkcja $f(n)$ jest $O(g(n))$, jeśli istnieją liczby dodatnie $c$ i $n_0$, takie że:

\[\forall_{n>n_0} ~~~~~ f(n) < c\cdot g(n)\]

Jeśli $f_1(n) \in O(g(n))$ i $f_2(n) \in O(g(n))$, to:

\[f_1(n) + f_2(n) \in O(g(n))$$ $$f_1(n) \cdot f_2(n) \in O(g^2(n))\]

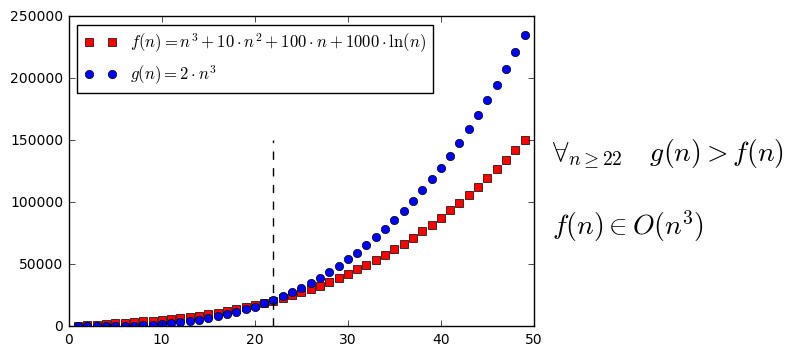
Notacja dużego Ο - przykład¶

import numpy as np
import matplotlib.pyplot as plt
from math import log

n = np.arange(1, 50, 1) # kolejne liczby naturalne
f = [n**3 + 10*n**2 + 100*n + 1000*log(n) for n in n] # wartości f(n)
g = [2*n**3 for n in n] # wartości g(n)

f_plot, = plt.plot(n, f, 'rs', label="$f(n) = n^3 + 10\cdot n^2 + 100\cdot n + 1000\cdot\ln(n)$")
g_plot, = plt.plot(n, g, 'bo', label="$g(n) = 2\cdot n^3$")

legend = plt.legend(handles=[f_plot, g_plot], loc=2)

line = plt.plot((22, 22), (0, 150000), 'k--')

label = plt.text(52, 75000, "$\\forall_{n\geq 22}$   $g(n) > f(n)$ \n\n"
                            "$f(n) \in O(n^3)$", fontsize=20)

plt.show()

png

Przykłady rzędów złożoności - $O(1)$¶

Proste operacje: arytmetyczne, logiczne, porównania, przypisania, dostęp do struktury danych

def constant(n):
    return n*n # jedna operacja -> O(1)

Przykłady rzędów złożoności - $O(n)$¶

def linear(n):
    result = 0 # 1 * operacja
    for element in n:     # n * operacja
        result += element # n * operacja
        result *= 0.1     # n * operacja
    return suma

ostatecznie mamy $3n + 1$ operacji, więc złożoność asymptotyczna -> $O(n)$

Przykłady rzędów złożoności - $O(n)$¶

def linear(n):
    for element in n:
        if element == 0:
            return True
    return False

złożoność asymptotyczna -> $O(n)$
może być lepsza (nawet $O(1)$), ale w najgorszym wypadku będzie n operacji

Przykłady rzędów złożoności - $O(n + m)$¶

def linear(n, m):
    result = 0

    for element in n:
        result += element

    for element in n:
        result += element

    return result

dwie pętle: $O(n)$ i $O(m)$
złożoność asymptotyczna $O(n+m)$

Przykłady rzędów złożoności - $O(n^2)$¶

def quadratic(n):
    result = 0
    for i in range(n):
        for j in range(i, n):
            result += 1
    return result

pętla zewnętrzna -> $n$ razy
pętla wewnętrzna -> $(n-i)$ razy
w sumie $1 + 2 + ... + n = \frac{n\cdot(n + 1)}{2} = \frac{1}{2}n^2 + \frac{1}{2}n$
złożoność asymptotyczna: $O(n^2) + O(n) = O(n^2)$

Przykłady rzędów złożności - $O(\log n)$¶

def logarithmic(n):
    result = 0
    while n > 1:
        n //= 2
        result += 1
    return result

w każdej iteracji zmniejszamy $n$ dwukrotnie
jeśli $n = 2^x$, to wykonamy $\log n$ operacji
algorytm jest $O(\log n)$

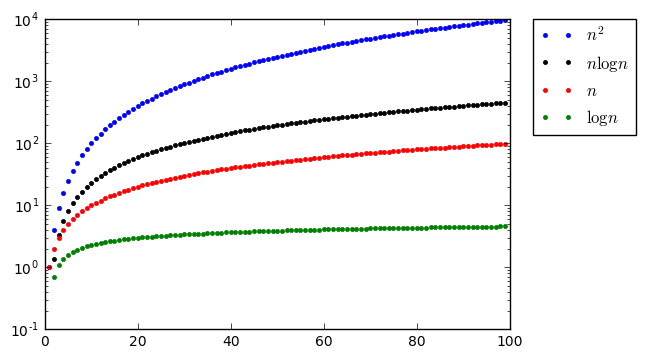
Porównanie złożoności¶

import numpy as np
import matplotlib.pyplot as plt
from math import log

n = np.arange(1, 100, 1)  # kolejne liczby naturalne
f = [n for n in n]        # zależność liniowa
g = [n**2 for n in n]     # zależność kwadratowa
h = [log(n) for n in n]   # zależność logarytmiczna
i = [n*log(n) for n in n] # zależność liniowo-logarytmiczna

g_plot, = plt.plot(n, g, 'b.', label="$n^2$")
i_plot, = plt.plot(n, i, 'k.', label="$n\log n$")
f_plot, = plt.plot(n, f, 'r.', label="$n$")
h_plot, = plt.plot(n, h, 'g.', label="$\log n$")

plt.yscale("log")

legend = plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)

plt.show()

png

# na wszelki wypadek do testów sortowania dużych tablic
import sys
sys.setrecursionlimit(10000)

Sortowanie bąbelkowe (bubble sort)¶

porównuj cyklicznie dwa sąsiadujące elementy
zmień kolejność jeśli zaburzają porządek
przerwij, jeśli nie ma co zmieniać

Sortowanie bąbelkowe - przykład¶

[3, 6, 4, 2] --> [3, 6, 4, 2] --> [3, 4, 6, 2] --> [3, 4, 2, 6]

[3, 4, 2, 6] --> [3, 4, 2, 6] --> [3, 2, 4, 6] --> [3, 2, 4, 6]

[3, 2, 4, 6] --> [2, 3, 4, 6] --> [2, 3, 4, 6] --> [2, 3, 4, 6]

[2, 3, 4, 6] --> [2, 3, 4, 6] --> [2, 3, 4, 6] --> [2, 3, 4, 6]

(brak zmian -> koniec)

Implementacja¶

def bubblesort(lst):
    """Sortuje podaną listę."""
    n = len(lst) # liczba elementów
    while True:  # powtarzaj do break
        swapped = False # ustaw flagę na fałsz
        for i in range(n-1): # pętla od 0 do n-2
            if lst[i] > lst[i+1]: # porządek zaburzony
                lst[i], lst[i+1] = lst[i+1], lst[i] # podmień
                swapped = True # ustaw flagę na prawdę
        if not swapped: # przerwij jeśli nie było zmian
            break

x = [3, 6, 4, 2]

bubblesort(x)

print(x)

[2, 3, 4, 6]

Krok po kroku¶

def bubblesort_v1(lst):
    """Sortuje podaną listę."""
    n = len(lst) # liczba elementów
    while True:  # powtarzaj do break
        swapped = False # ustaw flagę na fałsz
        print(lst, end=' ')
        for i in range(n-1): # pętla od 0 do n-2
            if lst[i] > lst[i+1]: # porządek zaburzony
                lst[i], lst[i+1] = lst[i+1], lst[i] # podmień
                swapped = True # ustaw flagę na prawdę
            print("->", lst, end=' ')
        print()
        if not swapped: # przerwij jeśli nie było zmian
            break

bubblesort_v1([3, 6, 4, 2])

[3, 6, 4, 2] -> [3, 6, 4, 2] -> [3, 4, 6, 2] -> [3, 4, 2, 6] 
[3, 4, 2, 6] -> [3, 4, 2, 6] -> [3, 2, 4, 6] -> [3, 2, 4, 6] 
[3, 2, 4, 6] -> [2, 3, 4, 6] -> [2, 3, 4, 6] -> [2, 3, 4, 6] 
[2, 3, 4, 6] -> [2, 3, 4, 6] -> [2, 3, 4, 6] -> [2, 3, 4, 6]

Optymalizacja I¶

def bubblesort_v2(lst):
    """Sortuje podaną listę."""
    n = len(lst) # liczba elementów
    while True:  # powtarzaj do break
        swapped = False # ustaw flagę na fałsz
        print(lst, end=' ')
        for i in range(n-1): # pętla od 0 do n-2
            if lst[i] > lst[i+1]: # porządek zaburzony
                lst[i], lst[i+1] = lst[i+1], lst[i] # podmień
                swapped = True # ustaw flagę na prawdę
            print("->", lst, end=' ')
        print()
        if not swapped: # przerwij jeśli nie było zmian
            break
        n -= 1 # n-te przejście -> n-ty największy na miejscu

bubblesort_v2([3, 6, 4, 2])

[3, 6, 4, 2] -> [3, 6, 4, 2] -> [3, 4, 6, 2] -> [3, 4, 2, 6] 
[3, 4, 2, 6] -> [3, 4, 2, 6] -> [3, 2, 4, 6] 
[3, 2, 4, 6] -> [2, 3, 4, 6] 
[2, 3, 4, 6]

Optymalizacja II¶

def bubblesort_v3(lst):
    """Sortuje podaną listę."""
    n = len(lst) # liczba elementów
    while n > 0:
        new_n = 0 # miejsce ostatniej zmiany
        print(lst, end=' ')
        for i in range(n-1): # pętla od 0 do n-2
            if lst[i] > lst[i+1]: # porządek zaburzony
                lst[i], lst[i+1] = lst[i+1], lst[i] # podmień
                new_n = i + 1 # indeks ostatniej zmiany
            print("->", lst, end=' ')
        print("new_n =", new_n)
        n = new_n # ostatnie przejście -> reszta musi być na miejscu

bubblesort_v3([3, 6, 4, 2])

[3, 6, 4, 2] -> [3, 6, 4, 2] -> [3, 4, 6, 2] -> [3, 4, 2, 6] new_n = 3
[3, 4, 2, 6] -> [3, 4, 2, 6] -> [3, 2, 4, 6] new_n = 2
[3, 2, 4, 6] -> [2, 3, 4, 6] new_n = 1
[2, 3, 4, 6] new_n = 0

Złożoność bubblesort¶

$n$ operacji -> co najmniej ostatni na swoim miejscu
$(n-1)$ operacji -> dwa ostatnie na swoim miejscu
$(n-2)$ operacji -> trzy na swoim miejscu itd...
$n + (n-1) + (n-2) + ... = O(n^2)$

Sortowanie przez scalanie (mergesort)¶

podziel nieposortowaną listę na $n$ "podlist" zawierających po jednym elemencie
cyklicznie scalaj "podlisty" w posortowane "podlisty", aż zostanie jedna

Start: [3, 6, 4, 2]

Split: [3] [6] [4] [2]

Merge: [3, 6] [2, 4]

Merge: [2, 3, 4, 6]

Algorytm scalania¶

mając dwie uporządkowane listy
porównaj skrajne elementy i mniejszy zapisz w liście wyjściowej
powtarzaj dopóki jedna z list się nie skończy
resztę dopisz na koniec wyjściowej listy

Algorytm scalania - przykład¶

[1, 6, 7] + [2, 3, 4, 5, 8, 9] --> [1]

[6, 7] + [2, 4, 5, 8, 9] --> [1, 2]

[6, 7] + [3, 4, 5, 8, 9] --> [1, 2, 3]

[6, 7] + [4, 5, 8, 9] --> [1, 2, 3, 4]

[6, 7] + [5, 8, 9] --> [1, 2, 3, 4, 5]

[6, 7] + [8, 9] --> [1, 2, 3, 4, 5, 6]

[7] + [8, 9] --> [1, 2, 3, 4, 5, 6, 7]

[] + [8, 9] --> [1, 2, 3, 4, 5, 6, 7, 8, 9]

Algorytm scalania - implementacja¶

def merge(A, B):
    """Scala posortowane listy zachowując porządek elementów."""
    result = [] # scalona lista
    while len(A) and len(B): # dopoki obie mają elementy
        # dodaj mniejszy element (usuwając go jednocześnie z listy)
        if A[0] < B[0]:
            result.append(A.pop(0))
        else:
            result.append(B.pop(0))

    result.extend(A) # dodaj resztę 
    result.extend(B) # (jeśli została)

    return result

merge([1, 6, 7], [2, 3, 4, 5, 8, 9])

[1, 2, 3, 4, 5, 6, 7, 8, 9]

Sortowanie przez scalanie - przykład¶

Start: [1, 4, 2, 5, 6, 3, 9, 7, 8]

Split: [1] [4] [2] [5] [6] [3] [9] [7] [8]

Merge: [1, 4] [2, 5] [3, 6] [7, 9] [8]

Merge: [1, 2, 4, 5] [3, 6, 7, 9] [8]

Merge: [1, 2, 3, 4, 5, 6, 7, 9] [8]

Merge: [1, 2, 3, 4, 5, 6, 7, 8, 9]

Sortowanie przez scalanie - implementacja¶

def mergesort(lst):
    """Sortuje podaną listę."""
    if len(lst) < 2: # lista jednoelementowa
        return lst   # nie wymaga sortowania

    middle = len(lst) // 2 # środek listy

    left = mergesort(lst[:middle])  # dziel na dwie części
    right = mergesort(lst[middle:]) # i wywołaj merge_sort (rekurencja)

    return merge(left, right) # scal dwie listy

mergesort([1, 4, 2, 5, 6, 3, 9, 7, 8])

[1, 2, 3, 4, 5, 6, 7, 8, 9]

Krok po kroku¶

def mergesort_p(lst):
    """Sortuje podaną listę."""
    if len(lst) < 2: # lista jednoelementowa
        return lst   # nie wymaga sortowania

    middle = len(lst) // 2 # środek listy

    left = mergesort_p(lst[:middle])  # dziel na dwie części
    right = mergesort_p(lst[middle:]) # i wywołaj merge_sort (rekurencja)

    # drukuj obecny stan
    # użyj kopii, żeby nie modyfikowac tablic
    print("left =", left, "\tright =", right,
          "\t-->", merge(left.copy(), right.copy()))

    return merge(left, right) # scal dwie listy

Krok po kroku¶

mergesort_p([1, 4, 2, 5, 6, 3, 9, 7, 8])

left = [1]  right = [4]     --> [1, 4]
left = [2]  right = [5]     --> [2, 5]
left = [1, 4]   right = [2, 5]  --> [1, 2, 4, 5]
left = [6]  right = [3]     --> [3, 6]
left = [7]  right = [8]     --> [7, 8]
left = [9]  right = [7, 8]  --> [7, 8, 9]
left = [3, 6]   right = [7, 8, 9]   --> [3, 6, 7, 8, 9]
left = [1, 2, 4, 5]     right = [3, 6, 7, 8, 9]     --> [1, 2, 3, 4, 5, 6, 7, 8, 9]





[1, 2, 3, 4, 5, 6, 7, 8, 9]

Złożoność mergesort¶

$\log_2 n + 1$ poziomów
na każdym $n$ operacji
złożoność czasowa -> $O(n\cdot\log n)$
złożoność pamięciowa -> $O(n)$

Sortowanie szybkie (quicksort)¶

wybierz element rozdzielający (pivot)
elementy nie większe przenieś "na lewo", resztę "na prawo"
powtórz rekurencyjnie dla części "lewej" i "prawej"

Sortowanie szybkie - przykład¶

[1, 4, 2, 5, 6, 3, 9, 7, 8] -> [1, 4, 2, 5, 3, 6, 9, 7, 8]

[1, 4, 2, 5, 3] -> [1, 2, 4, 5, 3]

[4, 5, 3] -> [4, 3, 5]

[4, 3] -> [3, 4]

[9, 7, 8] -> [7, 9, 8]

[9, 8] -> [8, 9]

Sortowanie szybkie - pivot¶

kluczowy jest wybór elementu rozdzielającego
przeciętnie, złożoność algorytmu $O(n\cdot\log n)$, gdy dzielimy dane na mniej więcej dwa równe podzbiory
gdy pivot jest wartością skrajną, to mamy jeden podzbiór $1$-elementowy i drugi $(n-1)$-elementowy; wtedy złożoność algorytmu $O(n^2)$

pivot - wybór¶

stały element: brzeg lub środek -> kiepski wybór
losowy -> teoretycznie kiepski, ale w praktyce się sprawdza
mediana -> dobry wybór, ale kosztowny
mediana z trzech -> mediana z pierwszego, ostatniego i środkowego

Implementacja quicksort¶

# "jednolinijkowy if"- niezalecany (na potrzeby slajdu)
def quicksort(lst):
    """Sortuje podaną listę."""
    if not len(lst): return lst # nie ma co sortować

    left, middle, right = [], [], [] # mniejsze, równe, większe

    pivot = lst[0] # kiepski wybór

    for x in lst:
        if x < pivot: left.append(x)
        elif x > pivot: right.append(x)
        else: middle.append(x)

    # wywołaj rekurencyjnie dla "lewej" i "prawej" części
    return quicksort(left) + middle + quicksort(right)

quicksort([1, 4, 2, 5, 6, 3, 9, 7, 8])

[1, 2, 3, 4, 5, 6, 7, 8, 9]

mergesort vs quicksort¶

import random

# 1000 losowych liczb od 0 do 999
x = random.sample(range(10000), 10000) 
y = x.copy()

%timeit -n3 quicksort(x)

3 loops, best of 3: 44.7 ms per loop

%timeit -n3 mergesort(y)

3 loops, best of 3: 114 ms per loop

%timeit -n3 quicksort(list(range(1000)))

3 loops, best of 3: 97.1 ms per loop

%timeit -n3 mergesort(list(range(1000)))

3 loops, best of 3: 5.73 ms per loop

bubblesort vs mergesort vs quicksort¶

def bubblesort(lst):
    """Sortuje podaną listę."""
    n = len(lst) # liczba elementów
    while n > 0:
        new_n = 0 # miejsce ostatniej zmiany
        for i in range(n-1): # pętla od 0 do n-2
            if lst[i] > lst[i+1]: # porządek zaburzony
                lst[i], lst[i+1] = lst[i+1], lst[i] # podmień
                new_n = i + 1 # indeks ostatniej zmiany
        n = new_n # ostatnie przejście -> reszta musi być na miejscu

def merge(A, B):
    """Scala posortowane listy zachowując porządek elementów."""
    result = [] # scalona lista
    while len(A) and len(B): # dopoki obie mają elementy
        # dodaj mniejszy element (usuwając go jednocześnie z listy)
        if A[0] < B[0]:
            result.append(A.pop(0))
        else:
            result.append(B.pop(0))

    result.extend(A) # dodaj resztę 
    result.extend(B) # (jeśli została)

    return result

def mergesort(lst):
    """Sortuje podaną listę."""
    if len(lst) < 2: # lista jednoelementowa
        return lst   # nie wymaga sortowania

    middle = len(lst) // 2 # środek listy

    left = mergesort(lst[:middle])  # dziel na dwie części
    right = mergesort(lst[middle:]) # i wywołaj merge_sort (rekurencja)

    return merge(left, right) # scal dwie listy

def quicksort(lst):
    """Sortuje podaną listę."""
    if not len(lst): # nie ma co sortować
        return lst

    left = []   # elementy mniejsze
    middle = [] # elementy równe
    right = []  # elementy większe

    pivot = lst[0] # kiepski wybór

    for x in lst:
        if x < pivot: left.append(x)
        elif x > pivot: right.append(x)
        else: middle.append(x)

    # wywołaj rekurencyjnie dla "lewej" i "prawej" części
    return quicksort(left) + middle + quicksort(right)

from timeit import timeit
import random

sizes = [10, 50, 100, 500, 1000, 5000, 10000]
bsort, msort, qsort = [], [], [] # wyniki timeit

for size in sizes:
    x = random.sample(range(size), size)
    y = x.copy()
    z = x.copy()

    bs = timeit("bubblesort(x)", number=1,
                setup="from __main__ import bubblesort, x")

    ms = timeit("mergesort(y)", number=1,
                setup="from __main__ import mergesort, y")

    qs = timeit("quicksort(z)", number=1,
                setup="from __main__ import quicksort, z")

    bsort.append(bs)
    msort.append(ms)
    qsort.append(qs)

bubblesort vs mergesort vs quicksort¶

import matplotlib.pyplot as plt

bs = plt.plot(sizes, bsort, 'bo', label="bubble")
ms = plt.plot(sizes, msort, 'ro', label="merge")
qs = plt.plot(sizes, qsort, 'go', label="quick")

plt.xscale("log")
plt.yscale("log")

legend = plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)

plt.show()

png

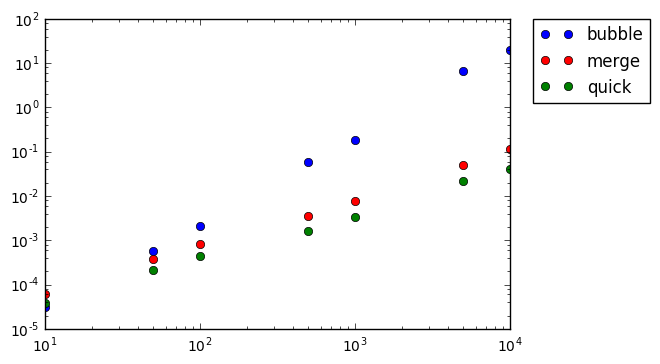
# css prezentacji

from IPython.display import display, HTML

s = """

<style>

.rendered_html code {
  font-size: 75%;
}

</style>

"""

display(HTML(s))

	Alg I	Alg II	Alg III	Alg IV	Alg V
operacje	\(n^2\)	\(n\)	\(1\)	\(n\)	n
pamięć	\(1\)	\(1\)	\(1\)	\(n\)	1
czas	4.6 s	973 \(\mu\)s	768 ns	661 \(\mu\)s	475 \(\mu\)s

Języki skryptowe - Python¶

Wykład 5¶

Dygresja o main¶

timeit¶

timeit z linii komend¶

timeit w Jupyter Notebook¶

Koty Ali¶

Koty Ali - algorytm I¶

Koty Ali - algorytm II¶

Koty Ali - algorytm III¶

Koty Ali - algorytm IV¶

range vs list(range)¶

Koty Ali - algorytm V¶

Złożoność algorytmu¶

Wartość wielomianu¶

Metoda naiwna¶

Schemat Hornera¶

Algorytm Hornera¶

Horner vs Naive¶

Złożoność algorytmów¶

Wkłady od różnych członów¶

Wkłady od różnych członów¶

Wkłady od różnych członów¶

Wkłady od różnych członów¶

Wkłady od różnych członów¶

Notacja dużego Ο¶

Notacja dużego Ο - przykład¶

Przykłady rzędów złożoności - \(O(1)\)¶

Przykłady rzędów złożoności - \(O(n)\)¶

Przykłady rzędów złożoności - \(O(n)\)¶

Przykłady rzędów złożoności - \(O(n + m)\)¶

Przykłady rzędów złożoności - \(O(n^2)\)¶

Przykłady rzędów złożności - \(O(\log n)\)¶

Porównanie złożoności¶

Sortowanie bąbelkowe (bubble sort)¶

Sortowanie bąbelkowe - przykład¶

Implementacja¶

Krok po kroku¶

Optymalizacja I¶

Optymalizacja II¶

Złożoność bubblesort¶

Sortowanie przez scalanie (mergesort)¶

Algorytm scalania¶

Algorytm scalania - przykład¶

Algorytm scalania - implementacja¶

Sortowanie przez scalanie - przykład¶

Sortowanie przez scalanie - implementacja¶

Krok po kroku¶

Krok po kroku¶

Złożoność mergesort¶

Sortowanie szybkie (quicksort)¶

Sortowanie szybkie - przykład¶

Sortowanie szybkie - pivot¶

pivot - wybór¶

Implementacja quicksort¶

mergesort vs quicksort¶

bubblesort vs mergesort vs quicksort¶

bubblesort vs mergesort vs quicksort¶