Machine Learning for MINERvA Physics Reconstruction

T. Golan

Warsaw, 11.01.2017

Navigate:
  PgDn / PgUp - next / previous slide
  Esc - expo mode

Outline

Main INjector ExpeRiment \(\nu\)-A

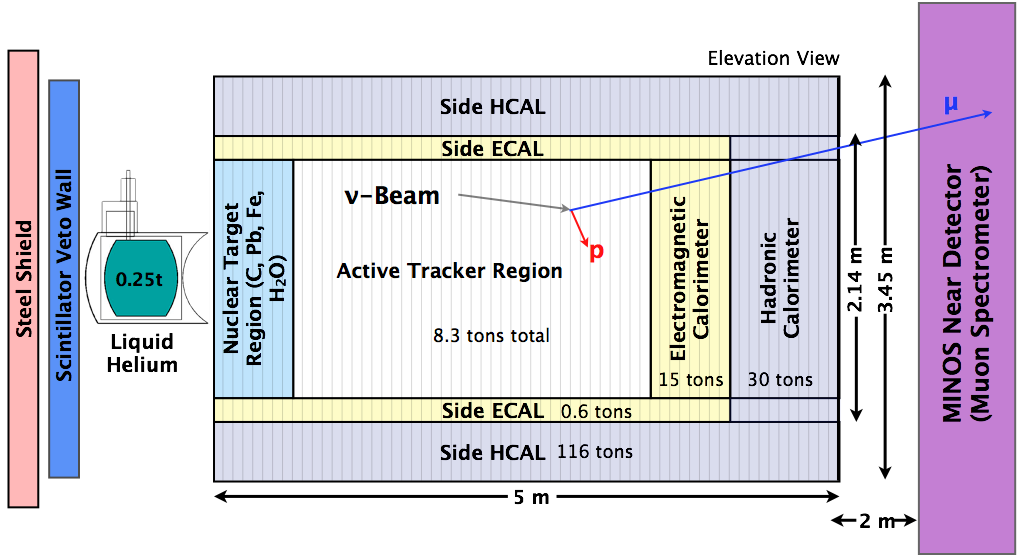
MINERvA Experiment

  • MINERvA is a neutrino-scattering experiment at Fermilab
  • Collaboration of about 50-100 physicist
  • NuMI beam is used to measure cross section for neutrino-nucleus interactions
  • The detector includes several different nuclear targets

Detector

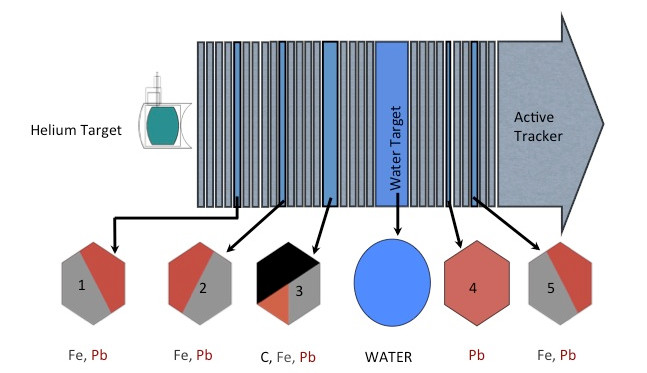
Nuclear targets

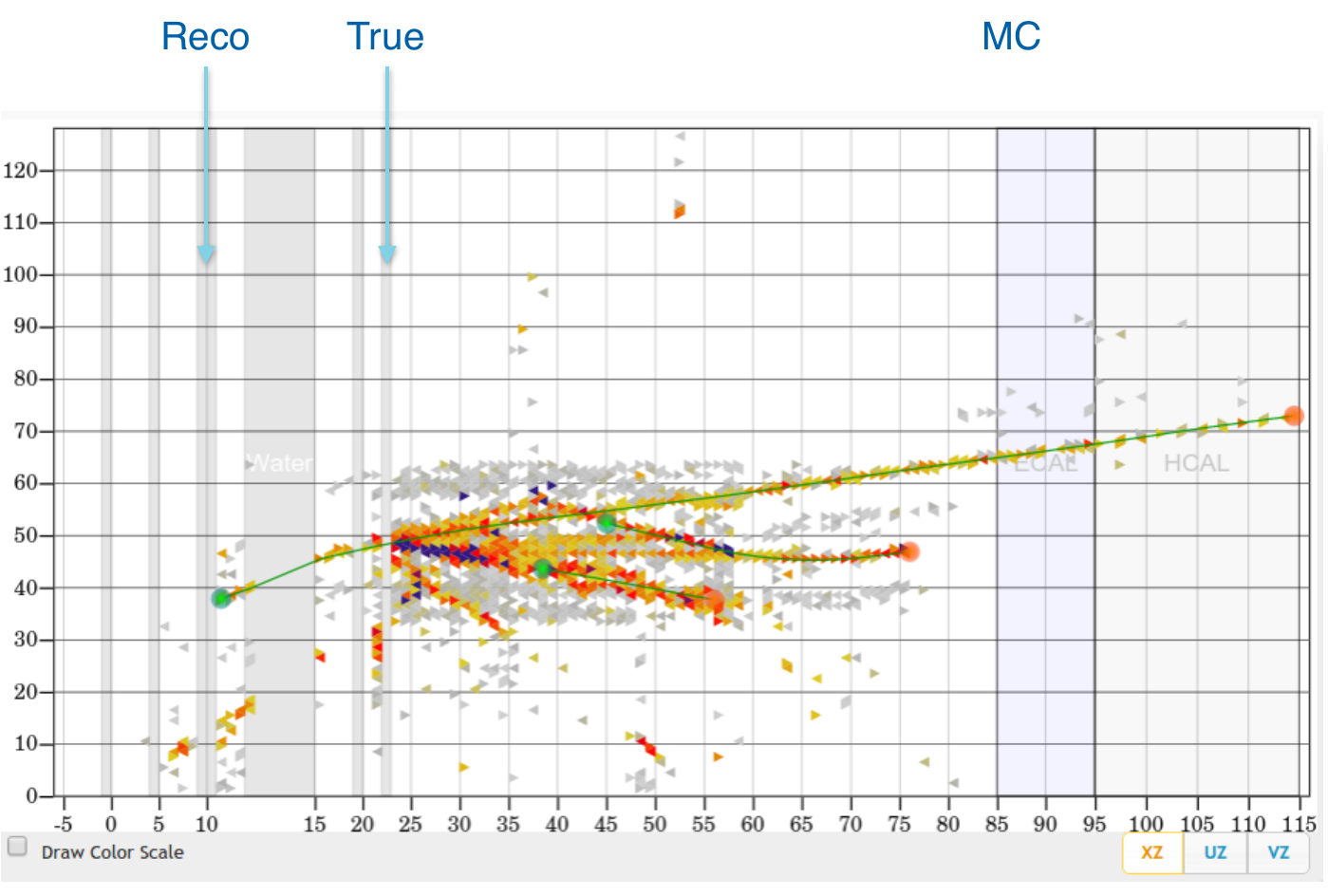
Event example 1


courtesy of G. Perdue

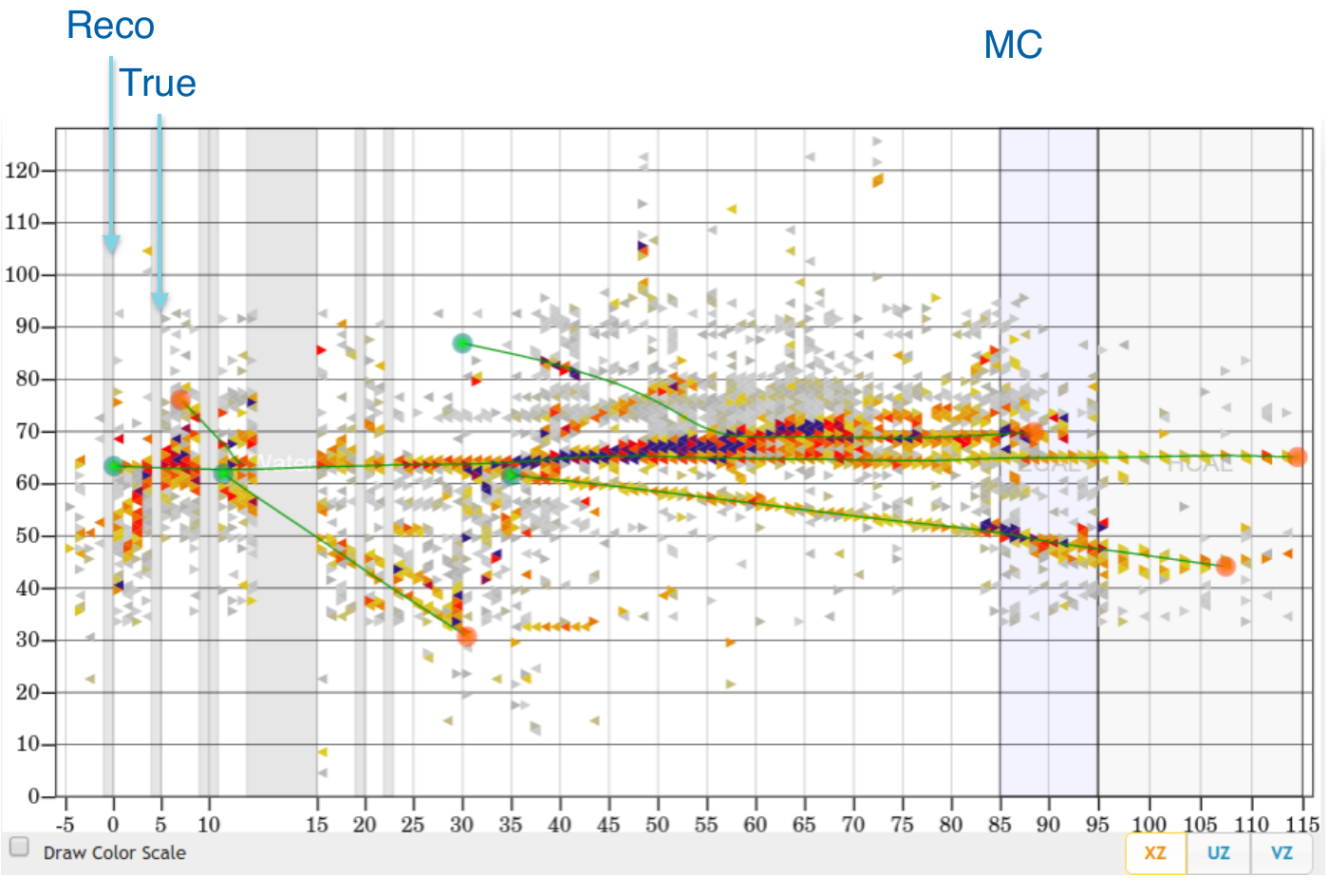
Event example 2


courtesy of G. Perdue

Vertex Reconstruction

  • tracking based algorithms fail for high energy events

  • "by eye" method is very often more accurate

  • idea: use algorithms for images analysis and pattern recognition

Machine Learning

Why ML?

  • ImageNet is an image database

  • Annual competition for classification
    • 2010: 71.8%
    • 2011: 74.3%
    • 2012: 84.0%
    • 2013: 88.2%
    • 2014: 93.3%
    • 2015: 96.4%
  • Humans: about 95%
  • Why humans fail?

Siberian Husky or Alaskan Malamute?

Understanding CNN

If you can't explain it simply, you don't understand it well enough.

Albert Einstein


Linear Regression

Notation

  • Hypothesis (for convenience \(x_0 = 1\)): \[h(x) = w_0 + w_1x_1 + ... + w_nx_n = \sum\limits_{i=0}^n w_i x_i = w^T x\]
  • Cost function: \[f(w) = \frac{1}{2}\sum\limits_{i=0}^n\left(h (x^{(i)}) - y^{(i)}\right)^2\]
  • Learning step (gradient descent, \(\alpha\) - training rate): \[w_j = w_j - \alpha\frac{\partial f(w)}{\partial w_j} = w_j + \alpha\sum\limits_{i=0}^n\left(y^{(i)} - h (x^{(i)})\right)x_j\]

Example


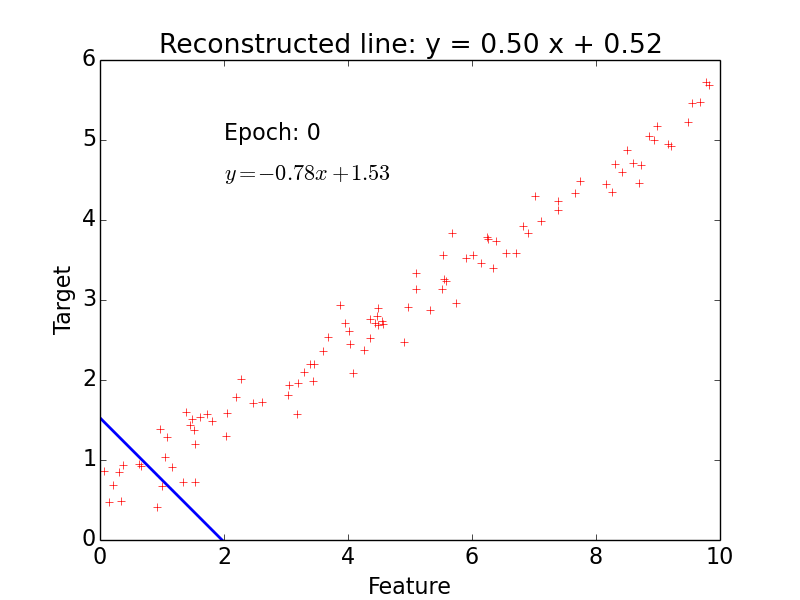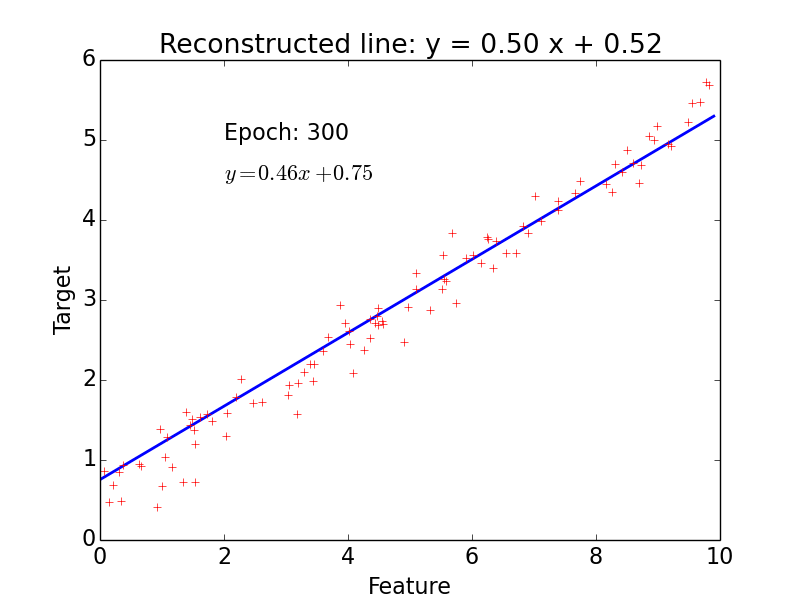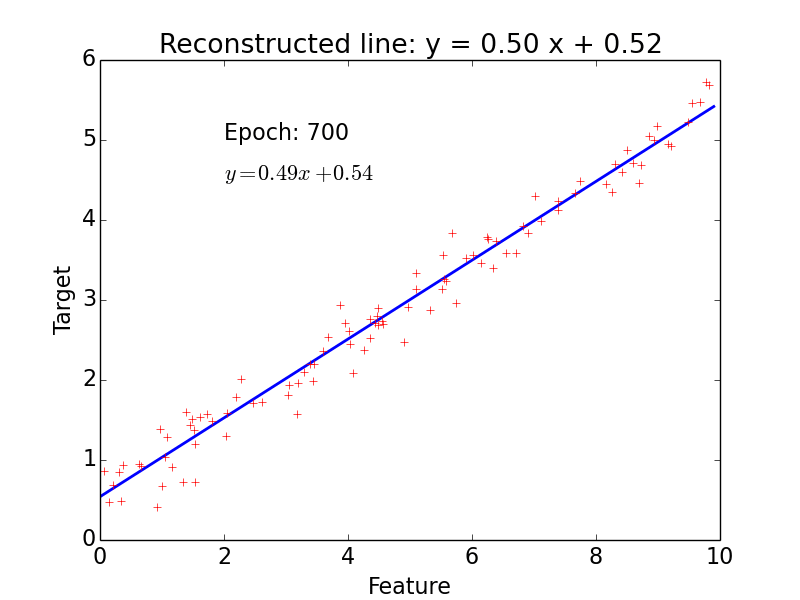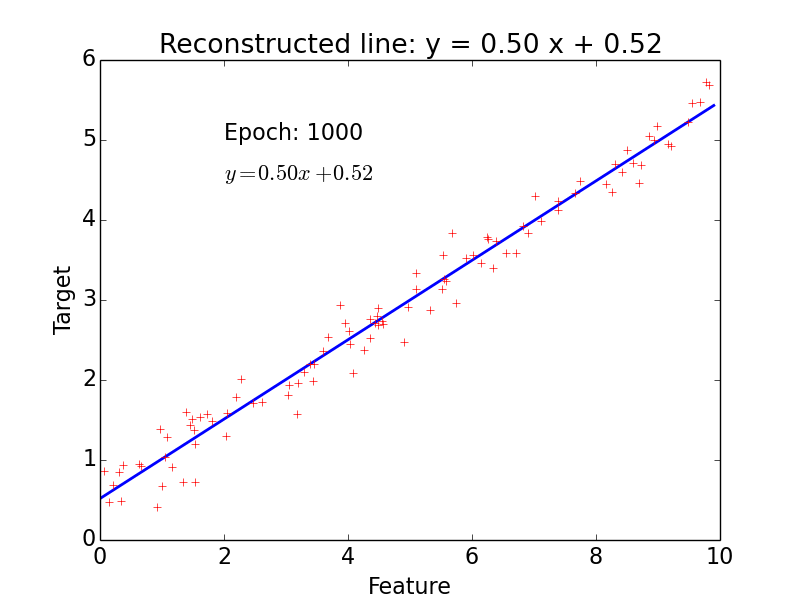
  • epoch = one loop over the whole training sample

  • for each feature vector weights are updated using gradient descent method

Classification


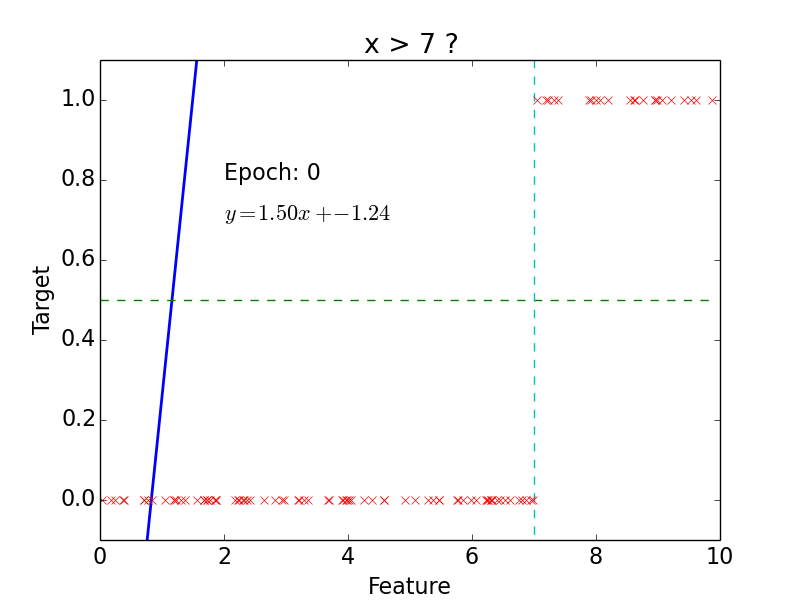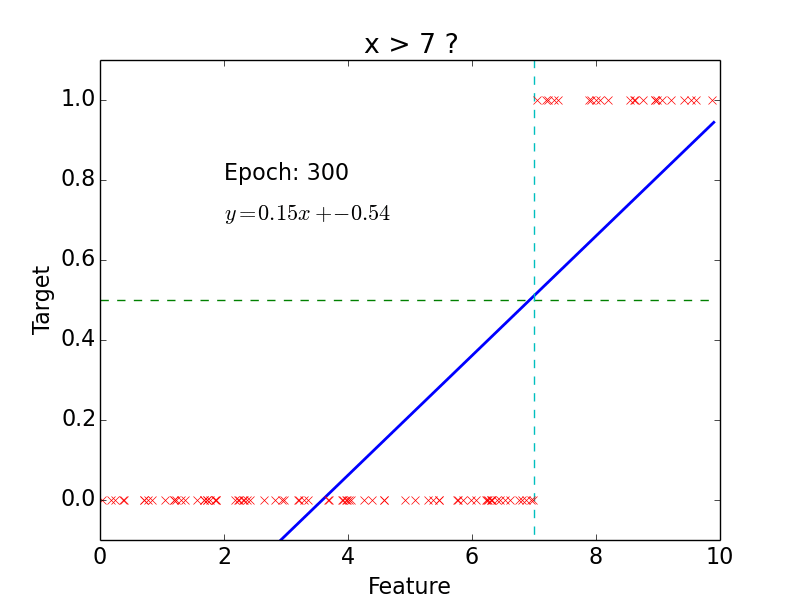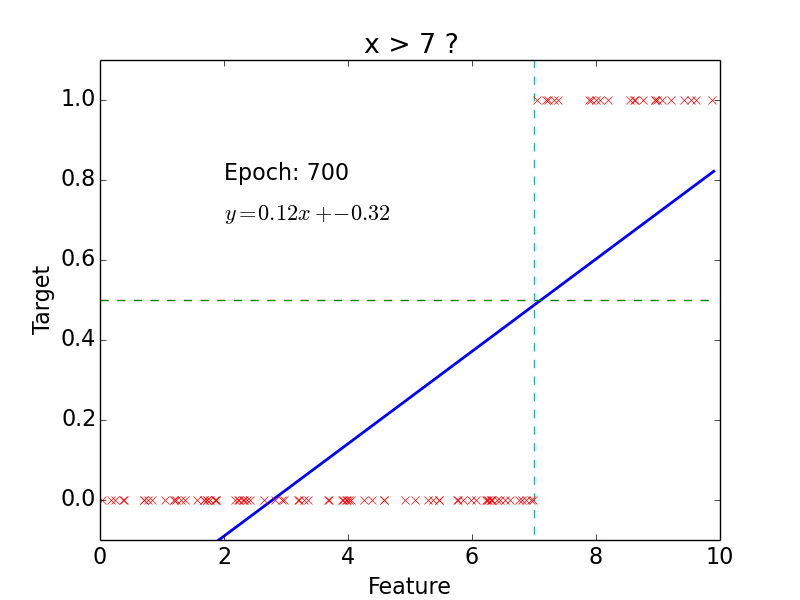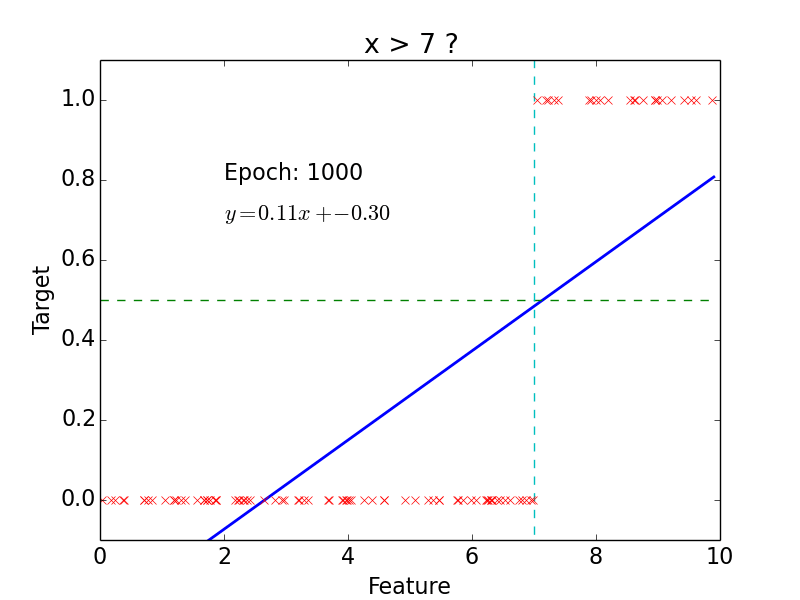
  • target: \(y = 0, 1\)

  • not really efficient for classification

  • imagine having some data ~ 100

  • logistic function does better job

Why do we need neural networks?

  • We can do classification

  • We can do regression

  • But real problems are nonlinear

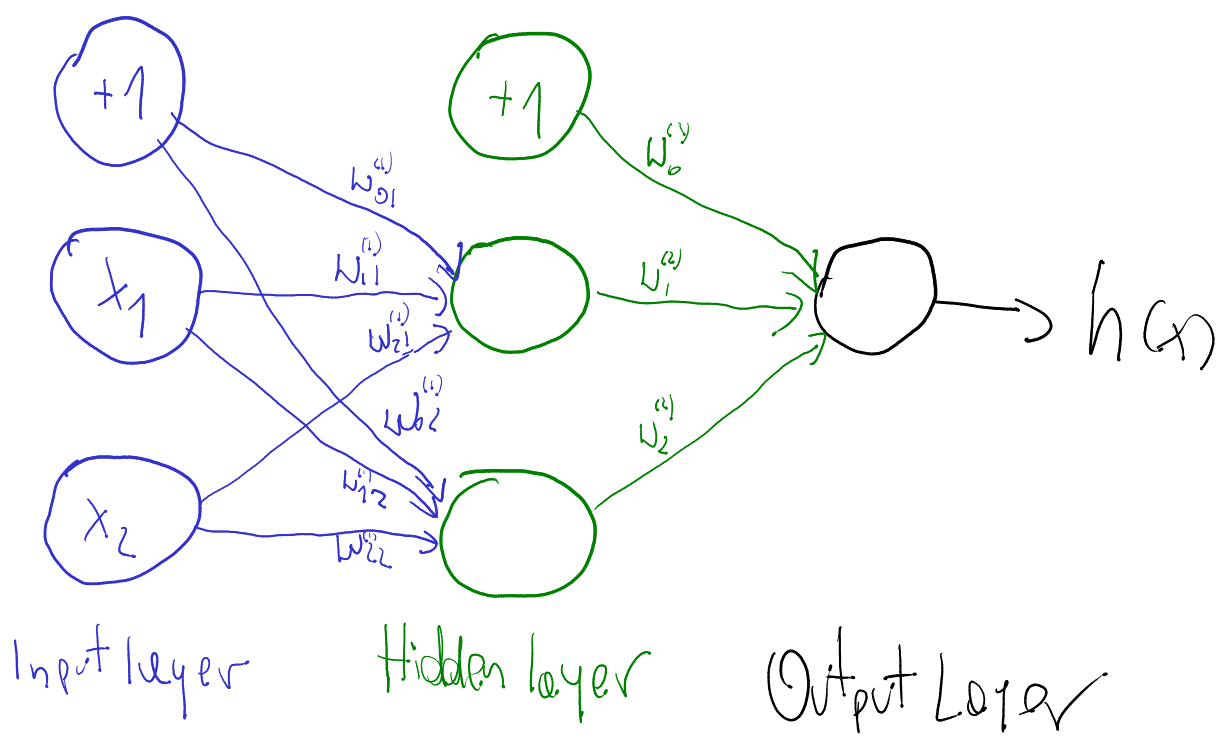
Neural Networks

Single Neuron


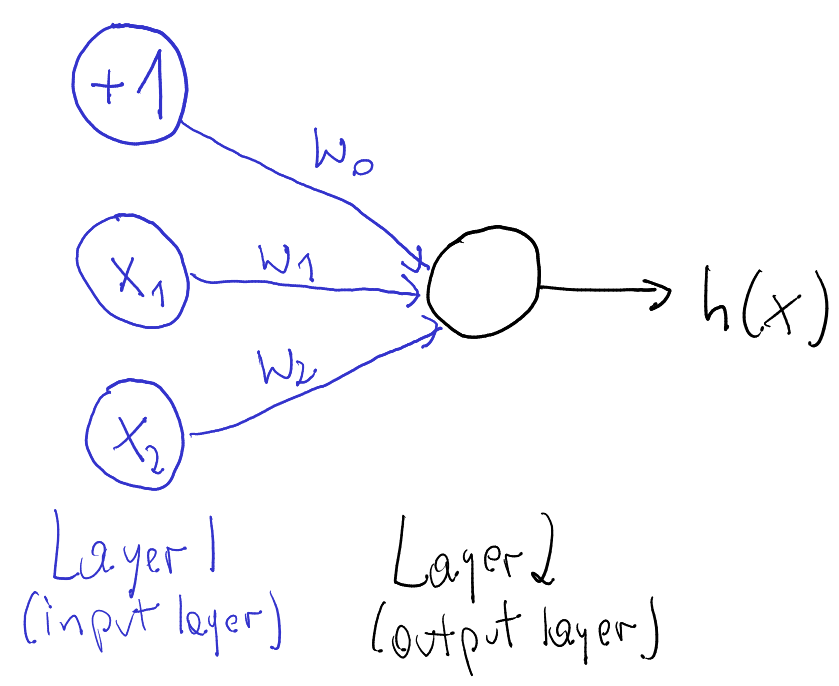
  • neuron = activation function:
    • linear
    • binary step
    • logistic
    • tanh
    • relu
    • ...
  • learned using gradient descent

Non-linear problem: XOR gate

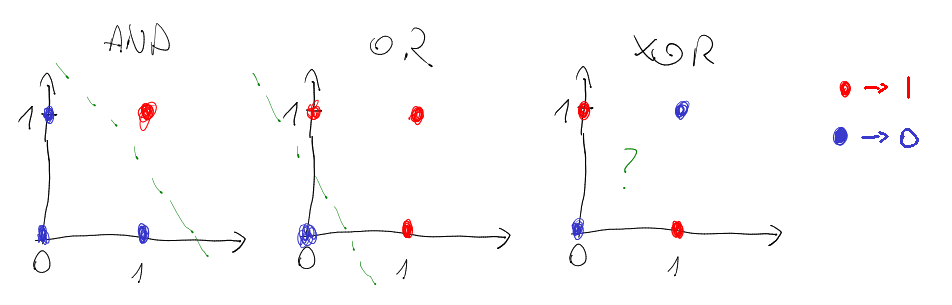
Neural network for XOR

x XOR y = (x AND NOT y) OR (y AND NOT x)

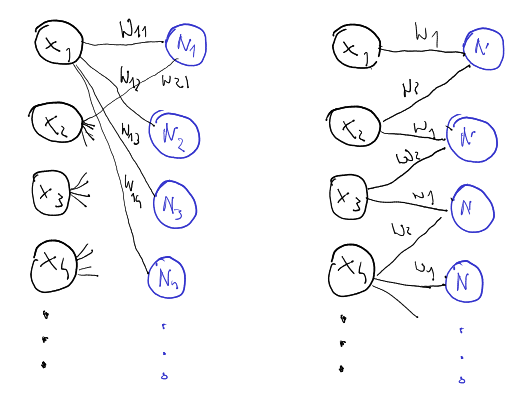
Neural Networks

  • more complicated problems require more neurons

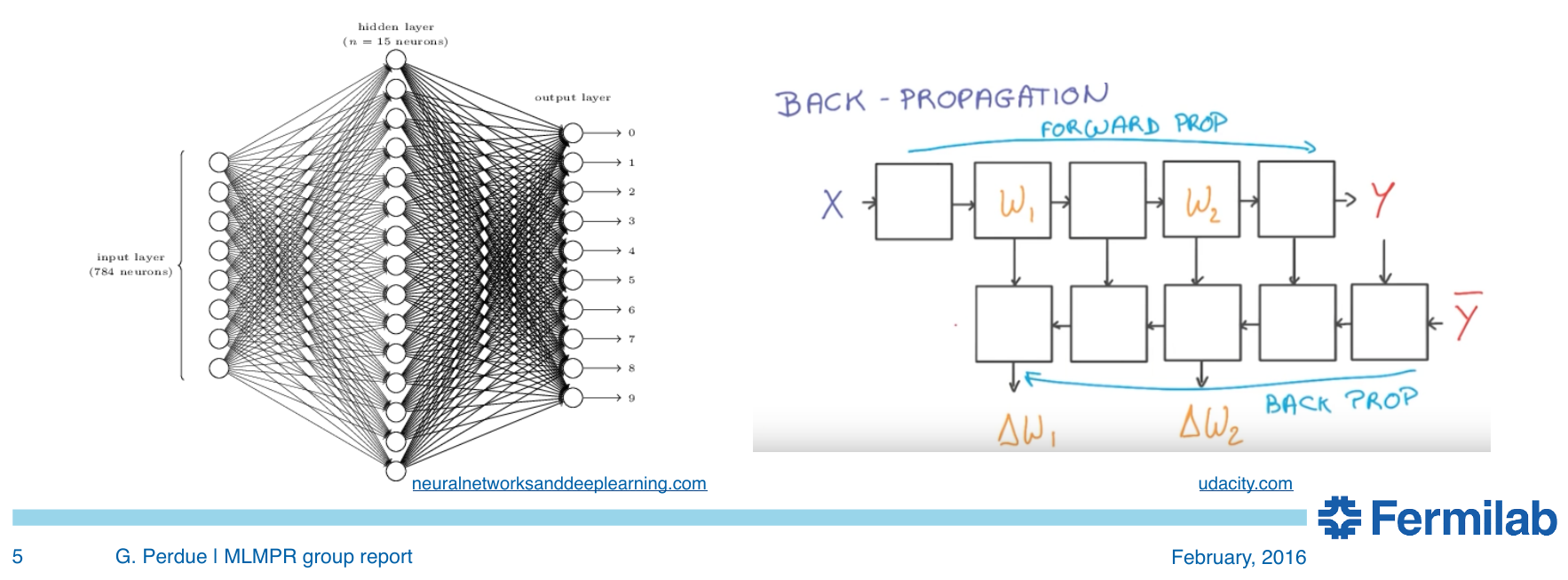
Convolutional Neural Networks

Idea

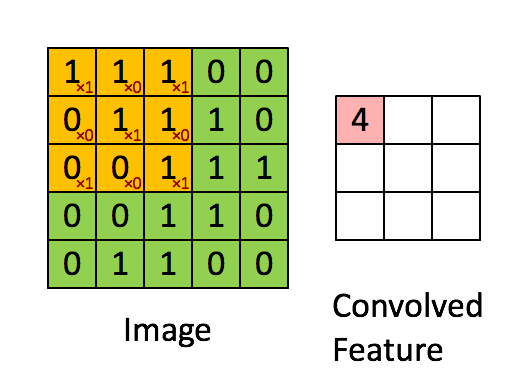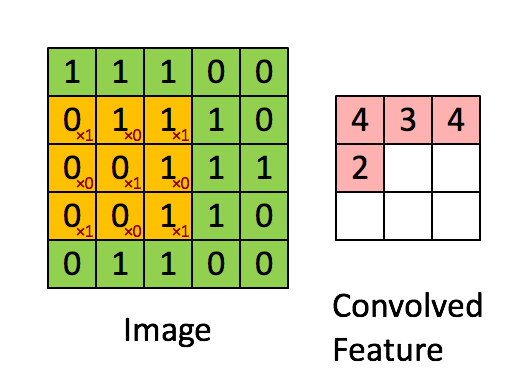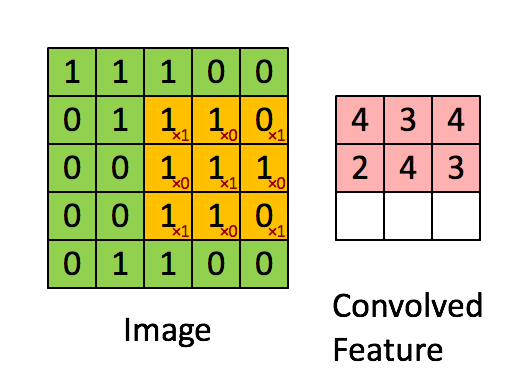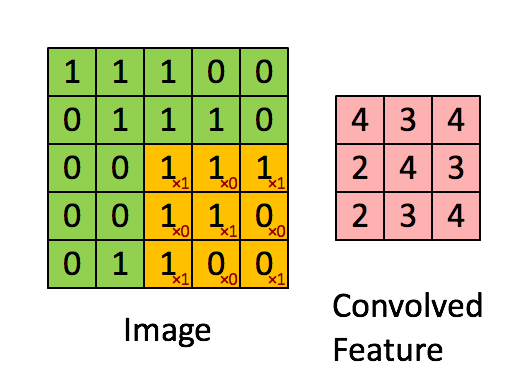
Convolution

src: deeplearning.net

"Clones" of a neuron looking at different part of an image

Convolution Layer

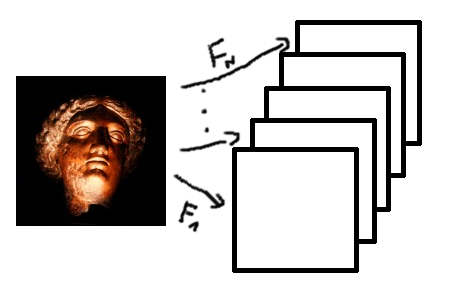
No. of convolved feature vectors / matrices = No. of filters

Pooling

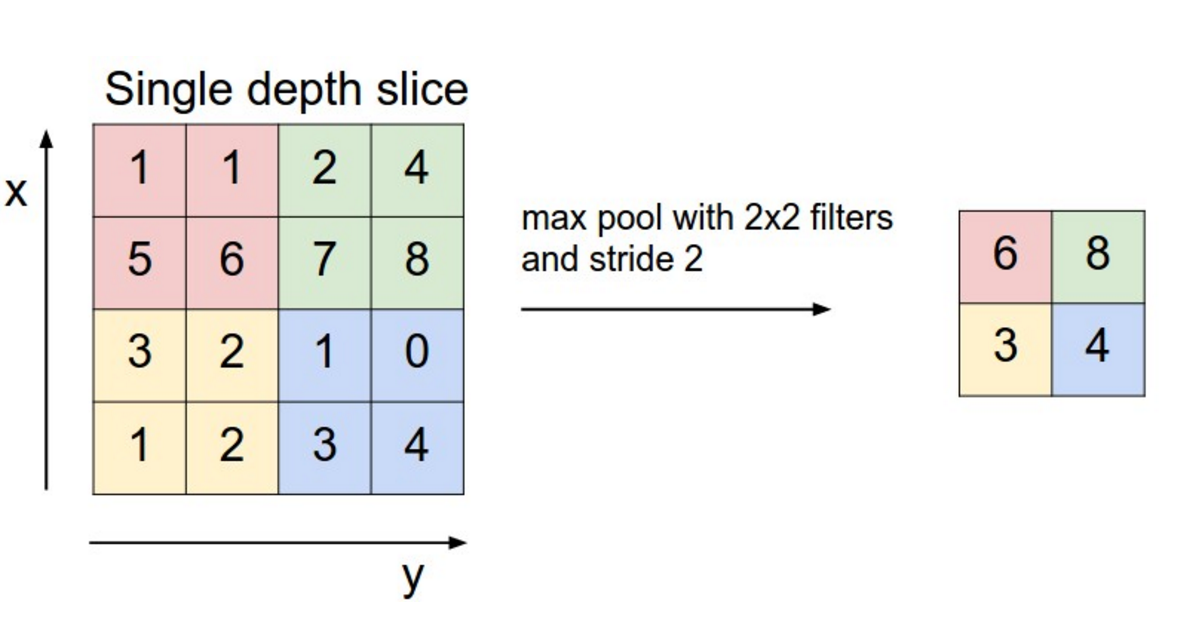
src: wildml.com

Pooling - example

src: arxiv

CNN example

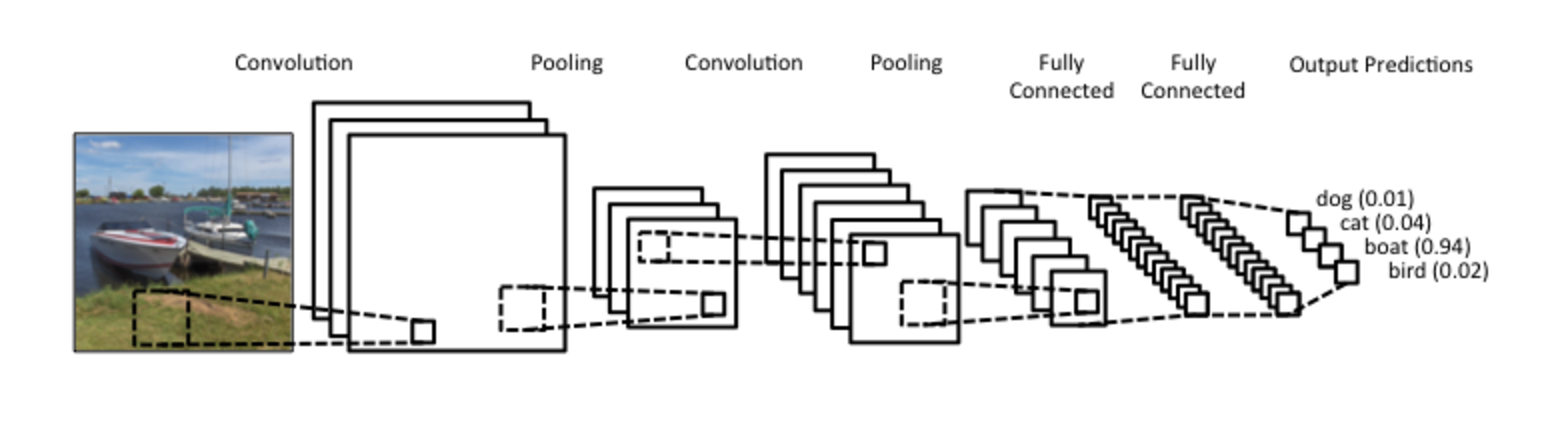
src: wildml.com

MLMPR First Attempts

What are we looking for?

  • The first goal is to use CNN to find vertex in nuclear target region

    • Classification: upstream of target 1, target 1, plastic between target 1 and target 2, target 2...

  • Next steps: NC\(\pi^0\)? \(\pi\) momentum? hadron multiplicities?

Classification regions


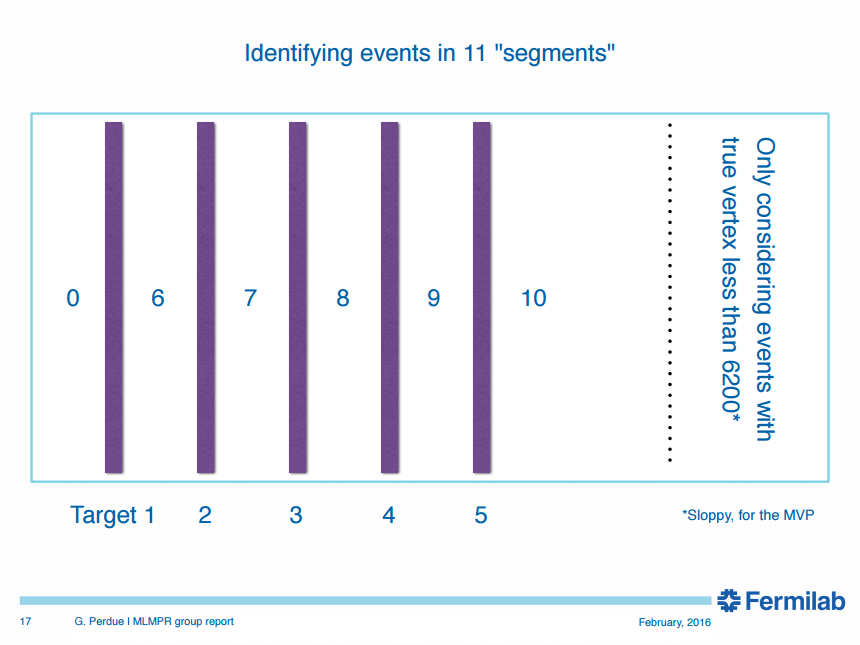
The current best

test accuracy:        92.67 %

    target 0 accuracy:            75.861 %
    target 1 accuracy:            94.878 %
    target 2 accuracy:            94.733 %
    target 3 accuracy:            93.596 %
    target 4 accuracy:            90.404 %
    target 5 accuracy:            94.011 %
    target 6 accuracy:            87.775 %
    target 7 accuracy:            85.225 %
    target 8 accuracy:            94.109 %
    target 9 accuracy:            53.077 %
    target 10 accuracy:           96.608 %


Purity * Efficiency (preliminary)

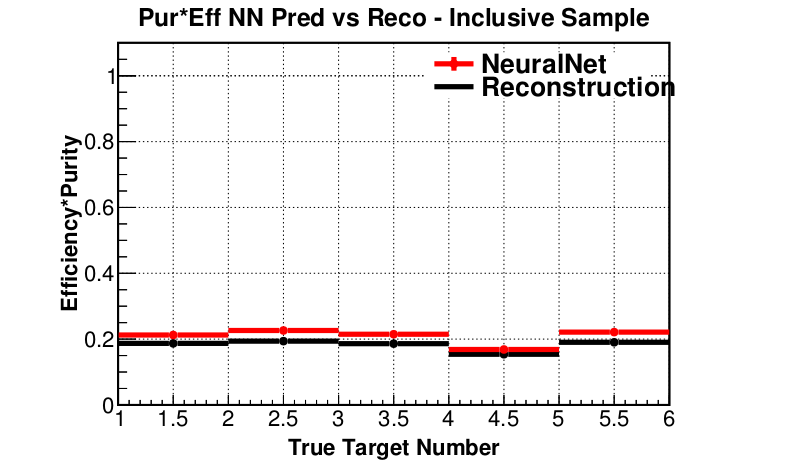
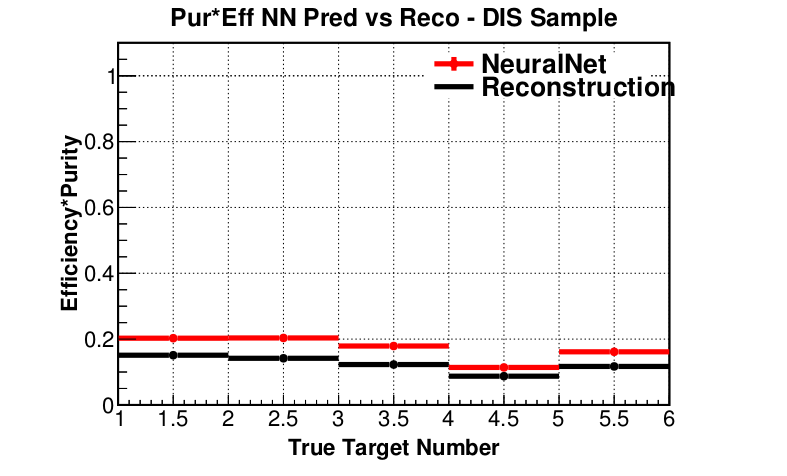
How did we get here?

In order to attain the impossible, one must attempt the absurd.

Miguel de Cervante

  • Some educated guesses
  • A little bit of intuition
  • And many, many attempts
  • ... on 2 GPU's
  • ... and later using Titan
  • Titan has 18,668 NVIDIA Kepler GPUs

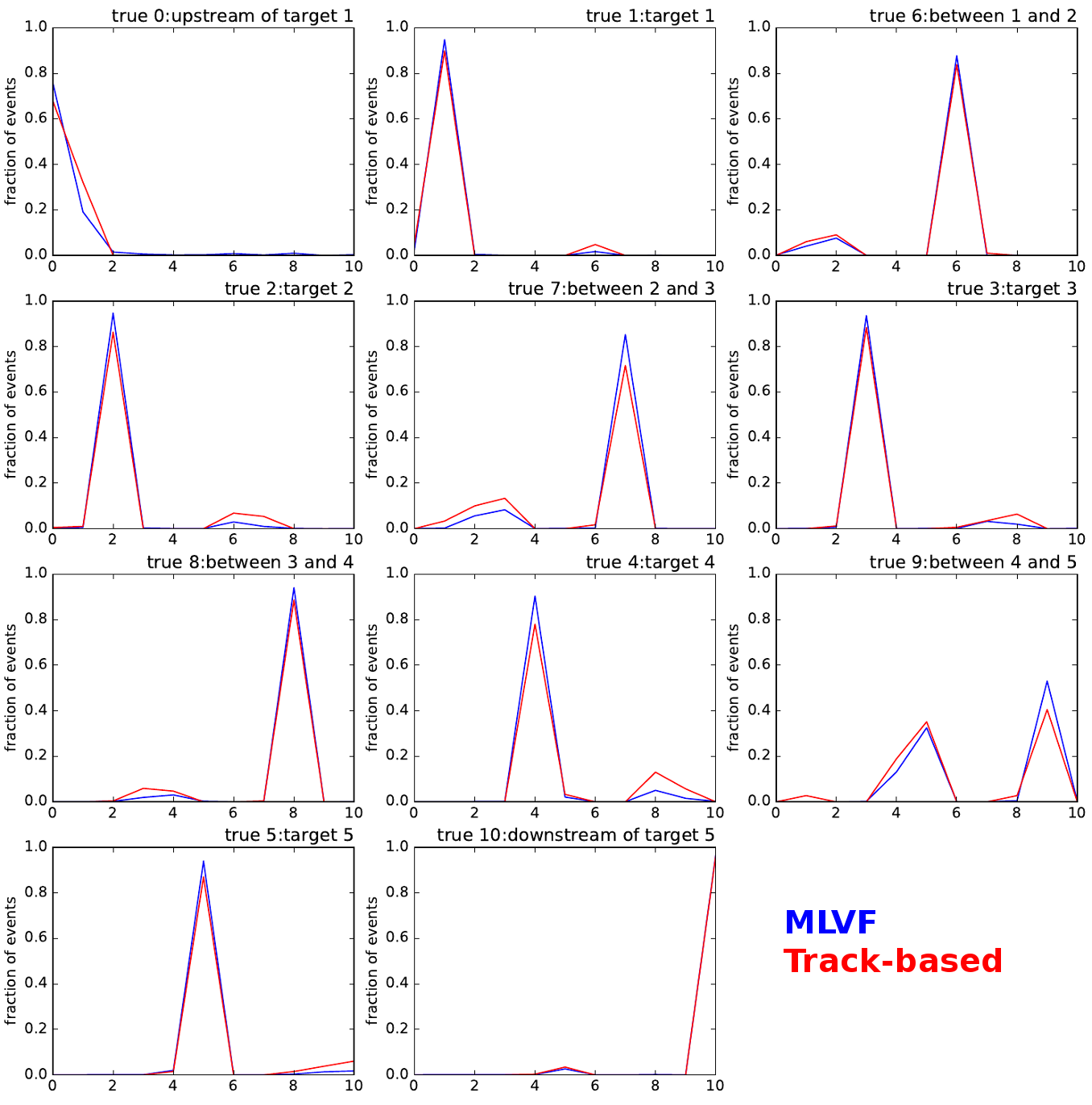
Summary

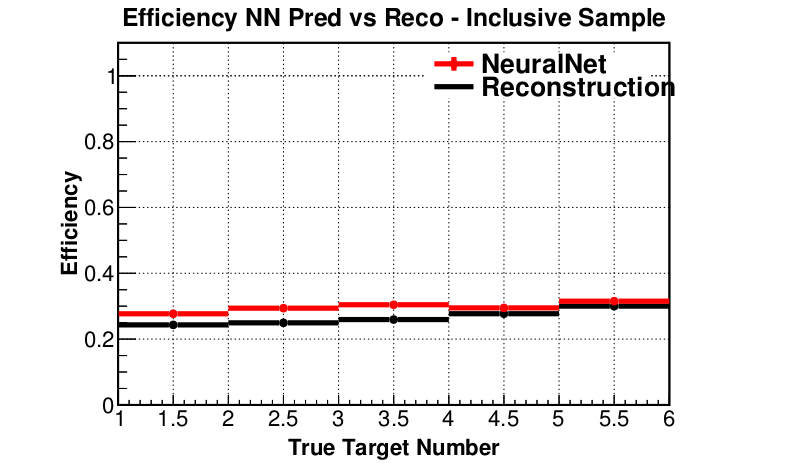
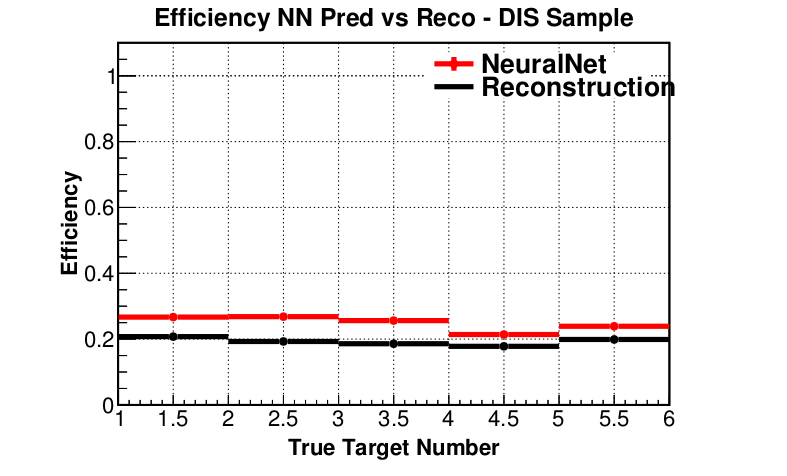
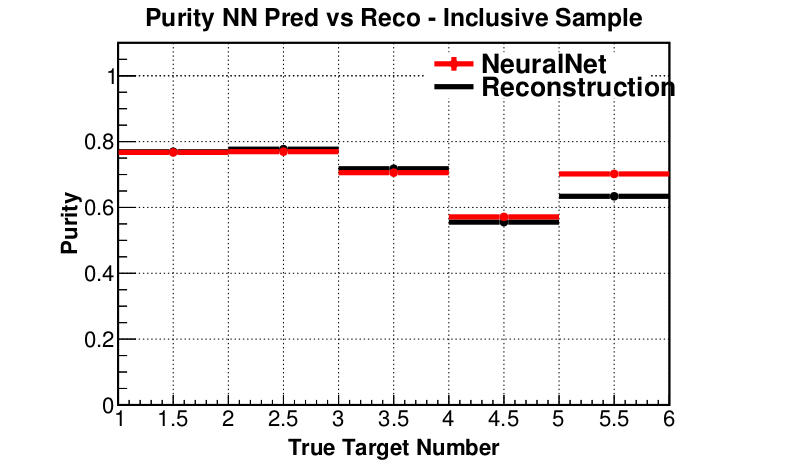
  • ML approach outperforms track-based reconstruction
  • Statistics, efficiency and purity is improved for inclusive and DIS samples
  • And this is just the beginning

Backup slides

Linear Classification

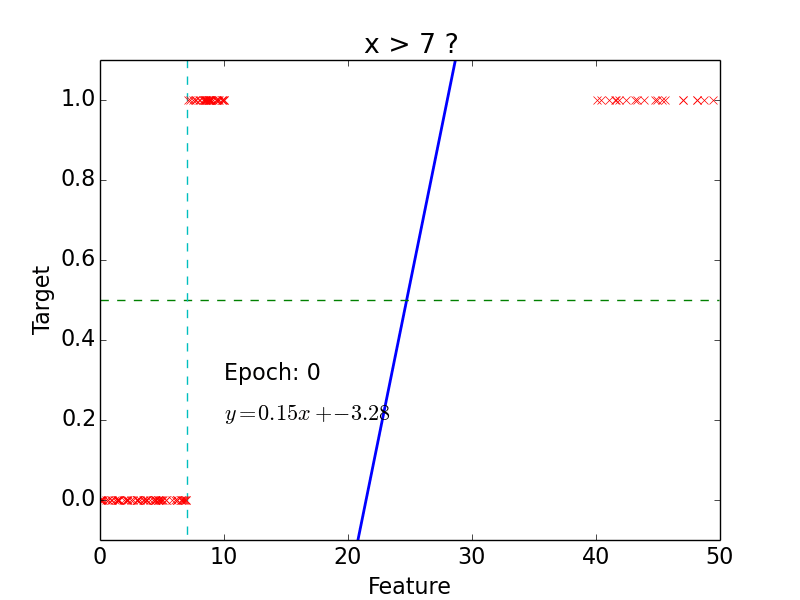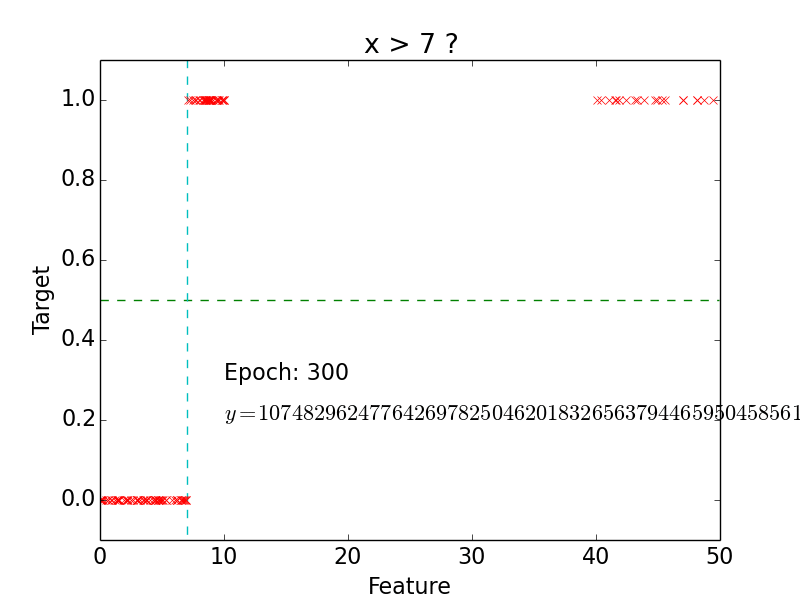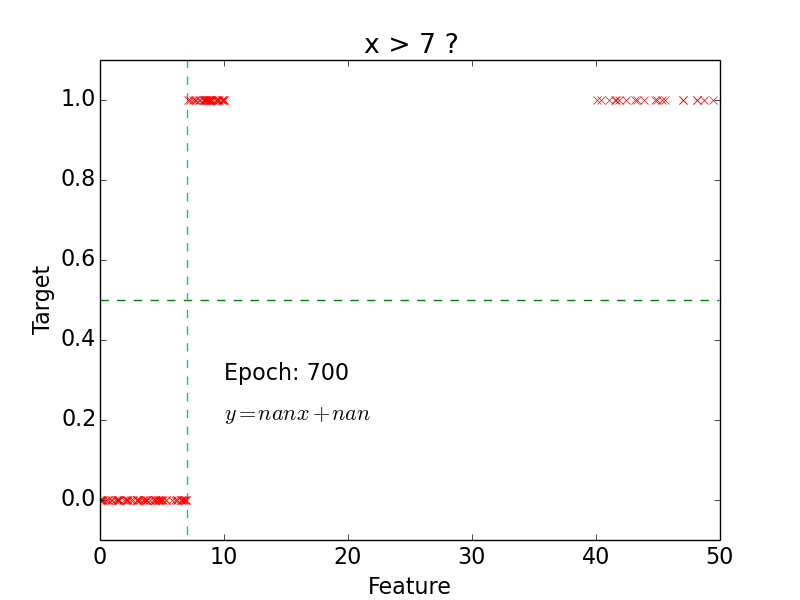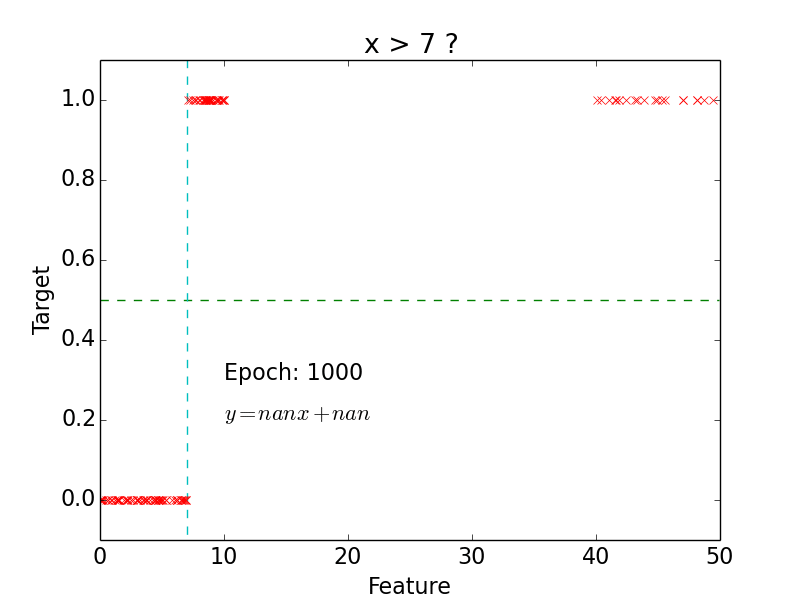
Logistic Regression

Logistic function


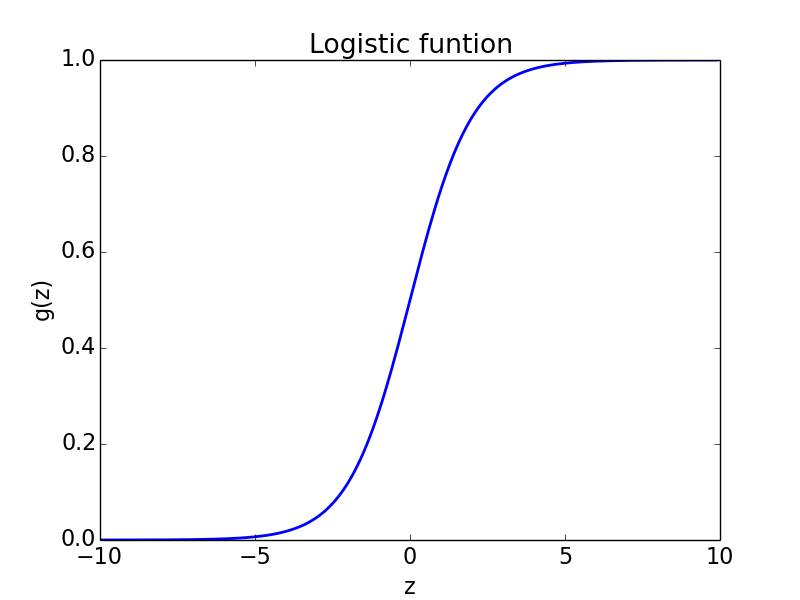
  • Logistic function: \[g(z) = \frac{1}{1 + e^{-z}}\]

  • Hypothesis: \[h(x) = g(w^Tx) = \frac{1}{1 + e^{-w^Tx}}\]

Classification

  • Probability of 1: \[P (y = 1 | x, w) = h(x)\]

  • Probability of 0: \[P (y = 0 | x, w) = 1 - h(x)\]

  • Probability: \[p (y | x, w) = (h(x))^y\cdot(1 - h(x))^{1 - y}\]

  • Likelihood: \[L(w) = \prod\limits_{i=0}^n p(y^{(i)} | x^{(i)}, w) = \prod\limits_{i=0}^n (h(x^{(i)}))^{y^{(i)}}\cdot(1 - h(x^{(i)}))^{1 - y^{(i)}}\]

  • Log-likelihood: \[l(w) = \log L(w) = \sum\limits_{i=0}^n y^{(i)}\log h(x^{(i)}) + (1 - y^{(i)})\log (1-h(x^{(i)}))\]

  • Learning step (maximize \(l(w)\)): \[w_j = w_j + \alpha\frac{\partial l(w)}{\partial w_j} = w_j + \alpha\sum\limits_{i=0}^n\left(y^{(i)} - h (x^{(i)})\right)x_j\]

Logistic Classification

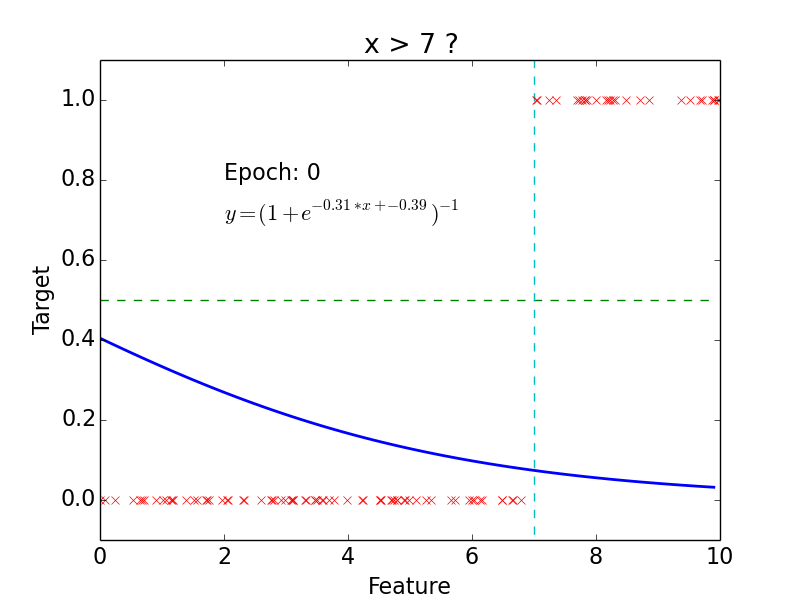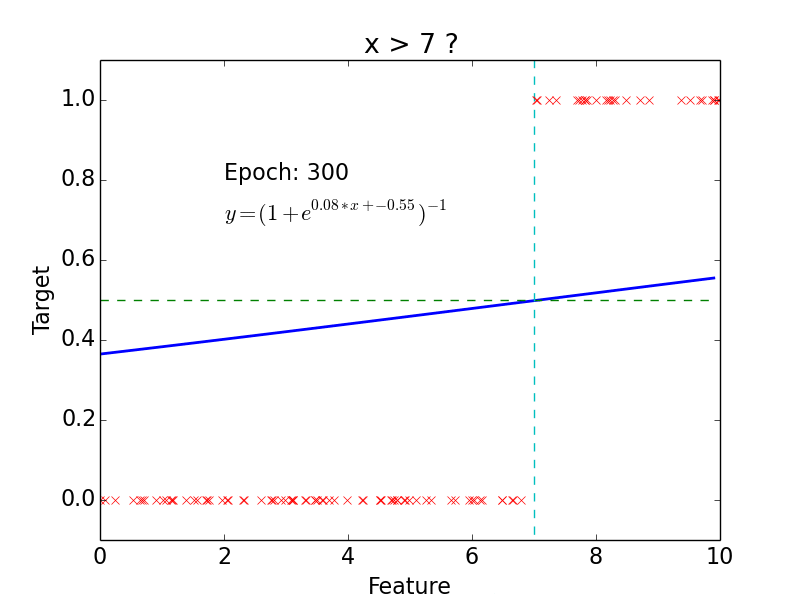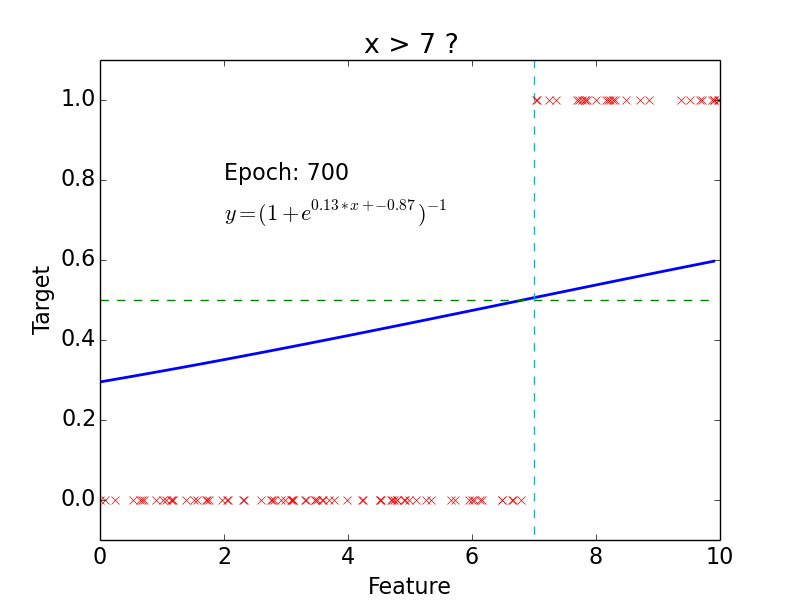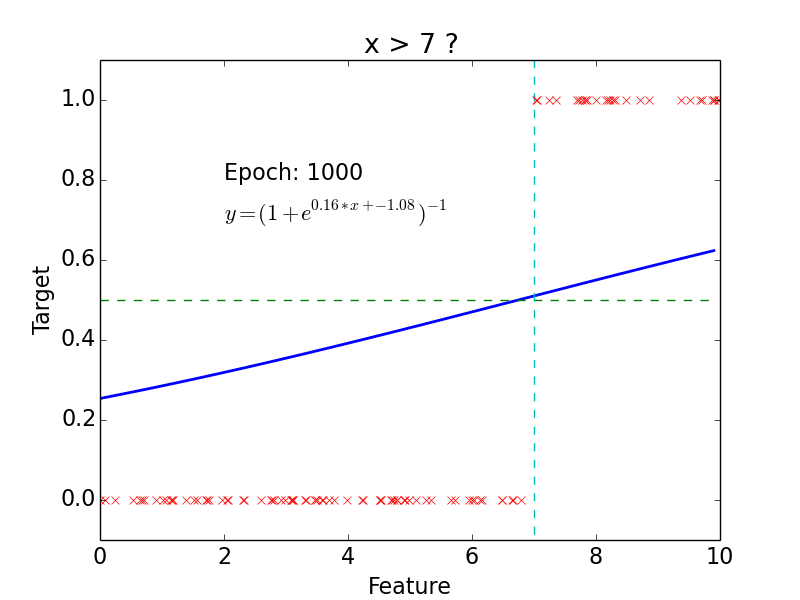
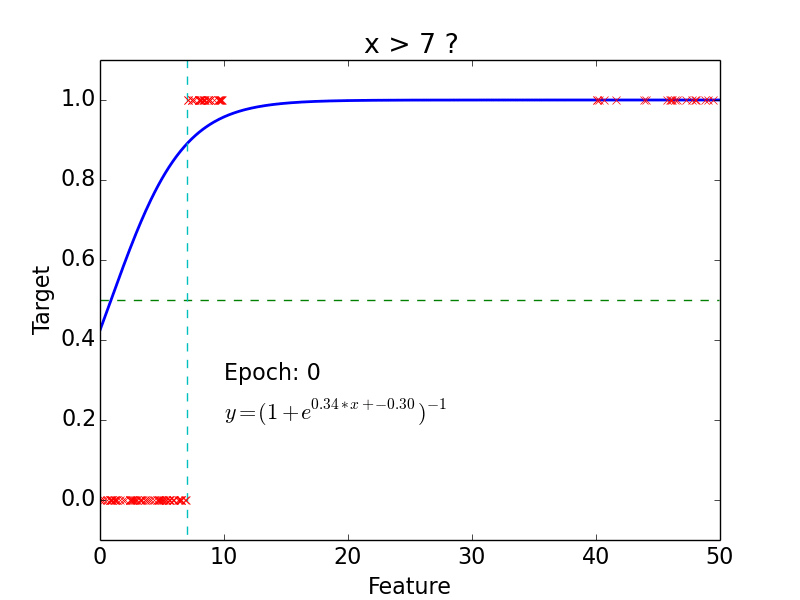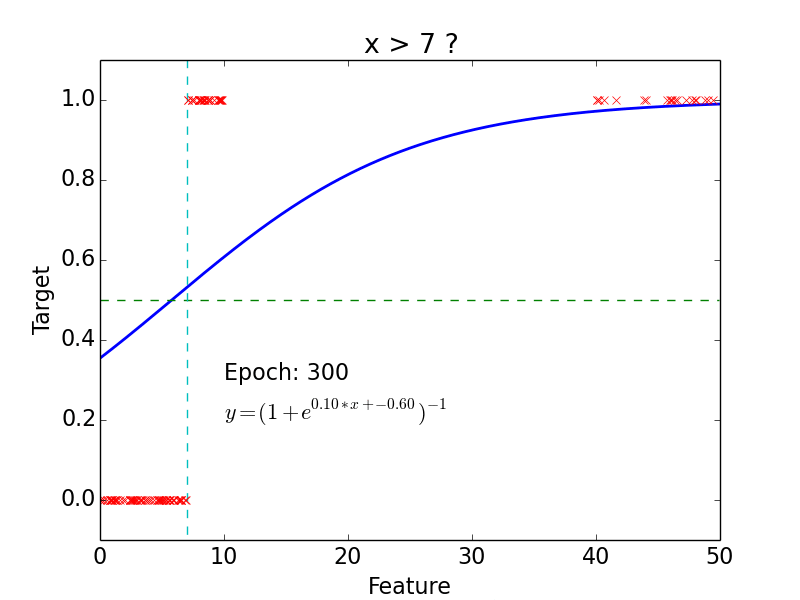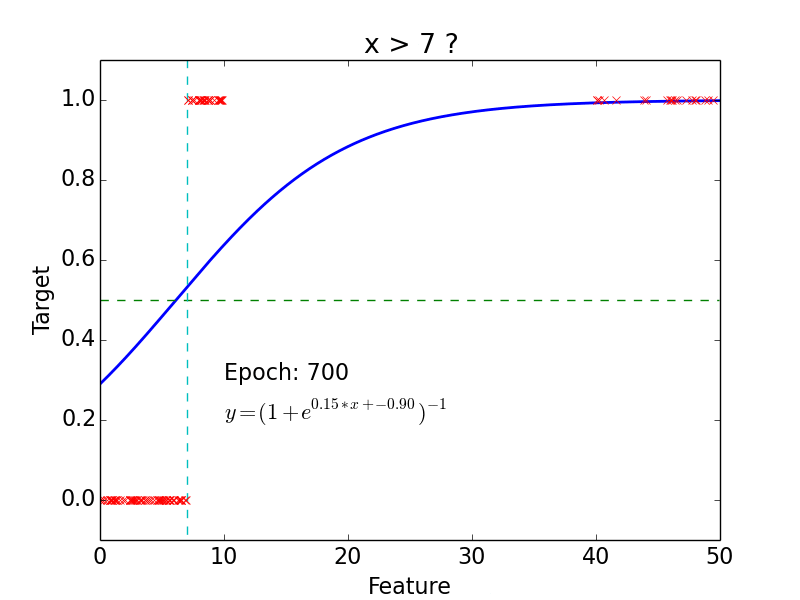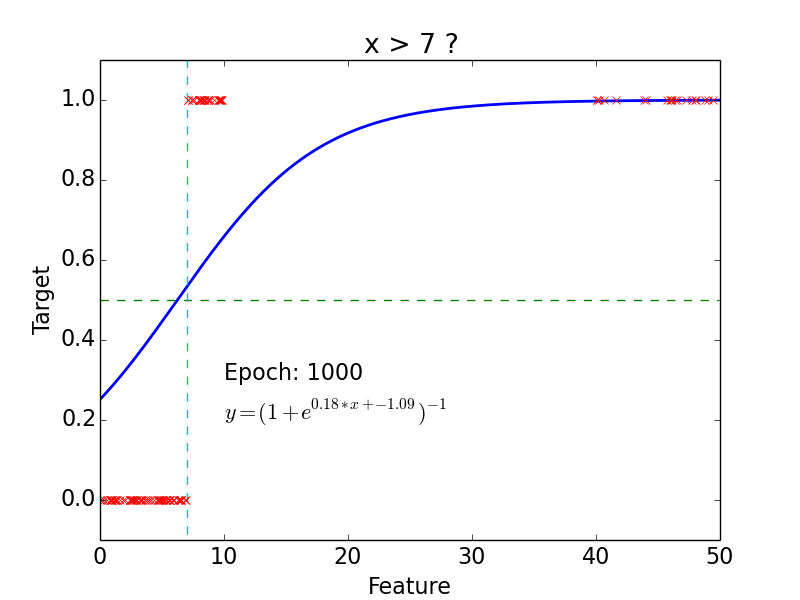
Non-linear problem

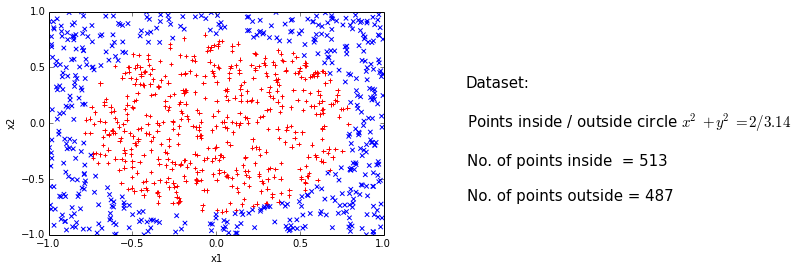
Trick

  • Feature vector: \[(x,y) \rightarrow (x,y,x^2,y^2)\]

  • Hypothesis: \[h (x) = \frac{1}{1 + e^{-w_0 - w_1x - w_2y - w_3x^2 - w_4y^2}}\]

In general, adding extra dimension by hand would be hard / impossible. Neural networks do that for us.

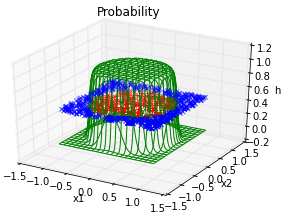
AND gate

\(x_1\) 0 1 0 1
\(x_2\) 0 0 1 1
AND 0 0 0 1


  • Hypothesis = logistic function:

\[h(x) = \frac{1}{1 + e^{-w^Tx}}\]

Intuition:

  • \(w_0 < 0\)
  • \(w_0 + w_1 < 0\)
  • \(w_0 + w_2 < 0\)
  • \(w_0 + w_1 + w_2 > 0\)

AND gate - learning

Purity (preliminary)

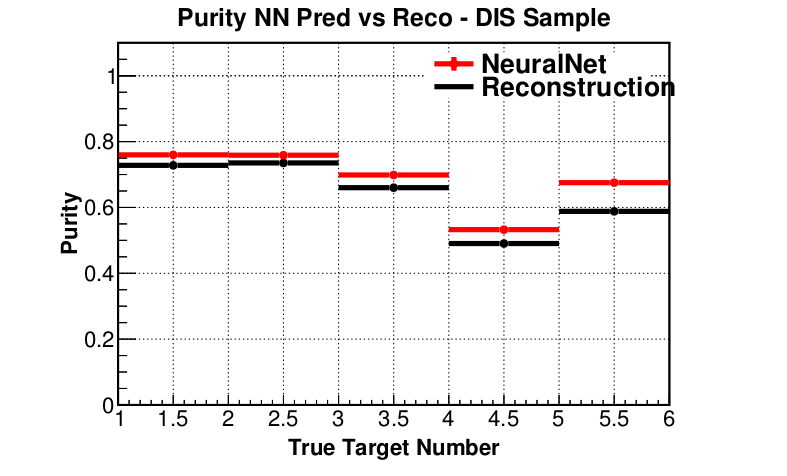
Efficiency (preliminary)