MINERvA Review
Tomasz Golan
Neutrino Seminar, 14.11.2016
Postdoc summary
University of Rochester
Department of Physics and Astronomy
MINERvA (prof. Kevin McFarland)
- flux systematic errors
- physics reconstruction using machine learning
- generator group coordinator
- production group leader
Fermi National Accelerator Laboratory
Scientific Computing Division
GENIE (dr. Gabe Perdue)
- nuclear effects in GENIE
- automated validation system
- "user support"
MINERvA Experiment
- MINERvA is a neutrino-scattering experiment at Fermilab
- Collaboration of about 50-100 physicist
- NuMI beam is used to measure cross section for neutrino-nucleus interactions
- The detector includes several different nuclear targets

Detector
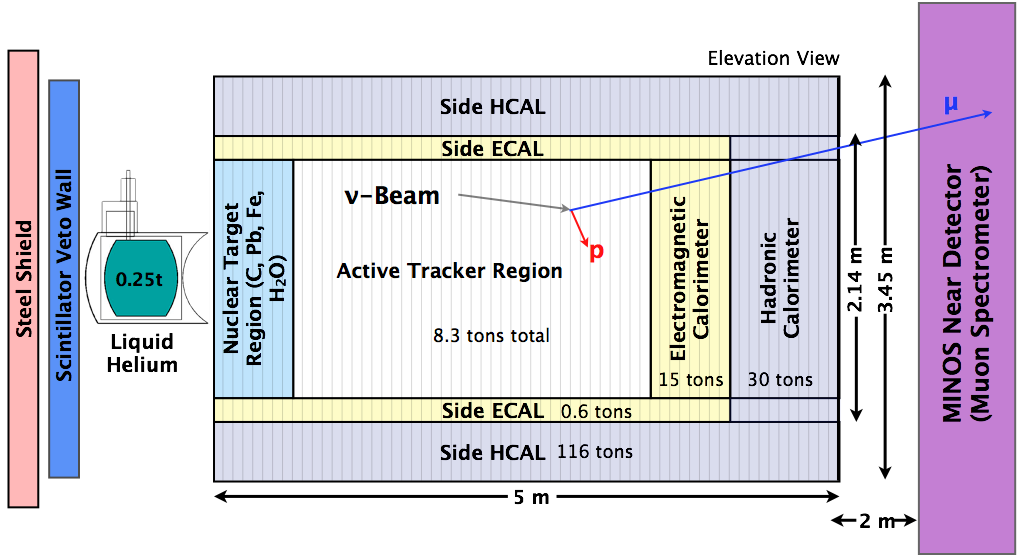
Nuclear targets
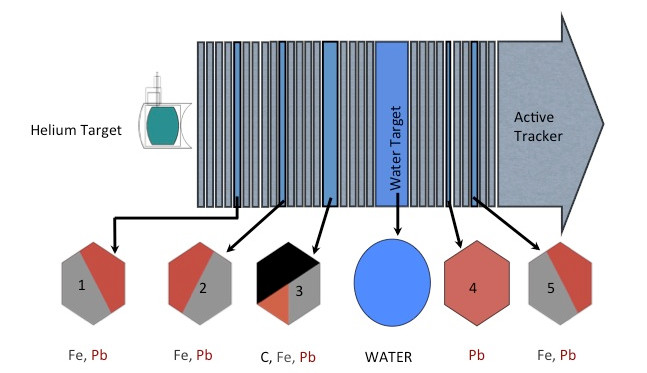
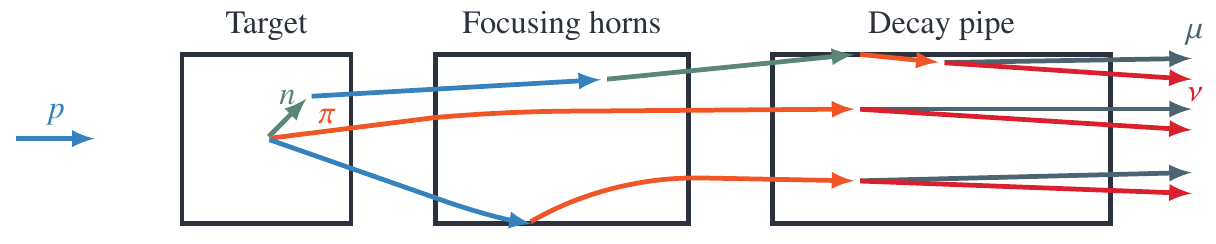
NuMI Beamline
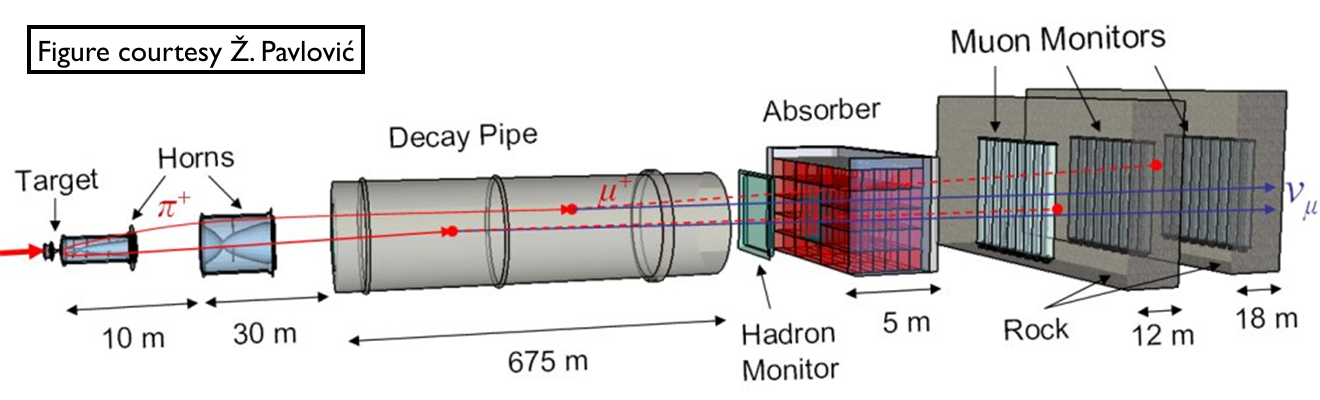
Low vs Medium Energy
by changing distance between horns one can change energy spectrum
by changing horns polarization one can switch between neutrino and anti-neutrino mode
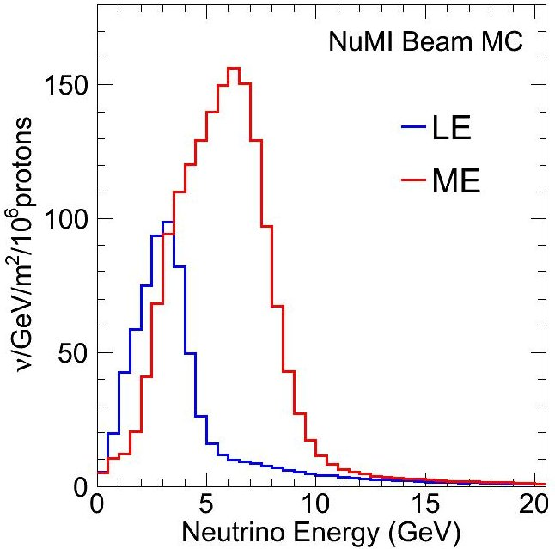
Flux
NuMI Beam Simulation
Flux simulation starts with a Geant4 with the NuMI geometry
All of the information about interactions leading to neutrino are stored
The results of the simulation are corrected by external data
Similar approach to the one T2K used
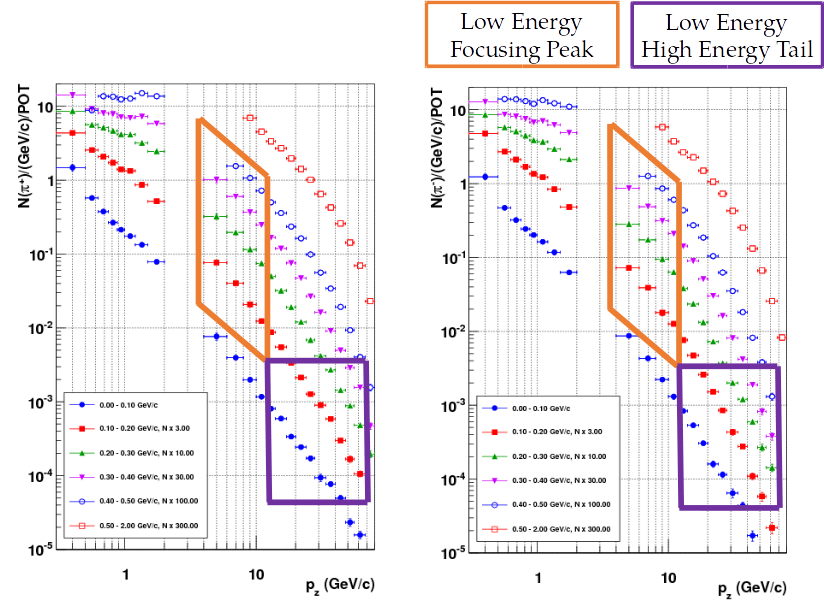
Hadron Scattering Data
NA49 - charged hadron production in proton scattering off thin targets
FLUKA is used to scale proton energy from \(158\) to \(120\) GeV
MIPP - charged hadron production on thin target and NuMI target replica
NA49 Data
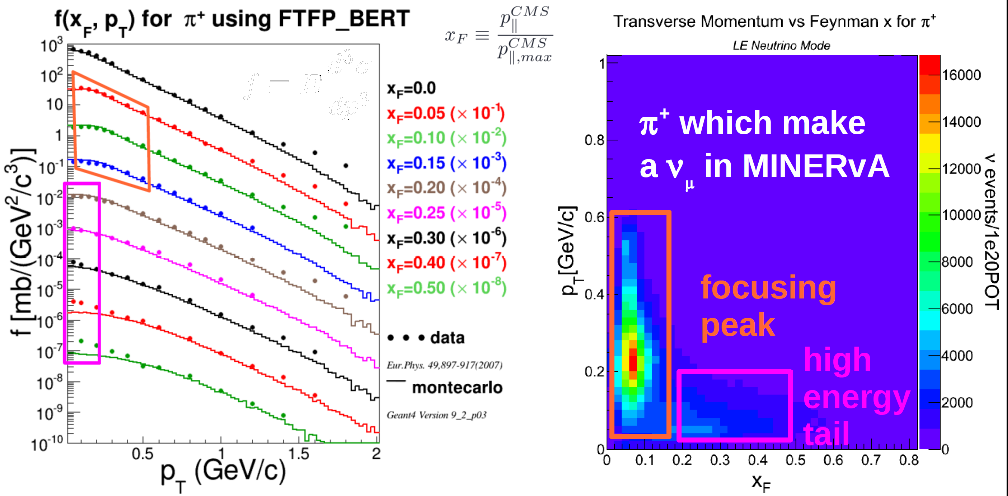
MIPP data
Reweighting
\[w_{HP} = \frac{f_{data}(x_F, p_T, E)}{f_{MC}(x_F, p_T, E)}, ~~~~~ f\equiv\frac{E}{\sigma}\frac{d^3\sigma}{dp^3}\]
Using external hadron production data events are weighted using the above formula
An event is reweighted on "interaction-by-interaction" basis
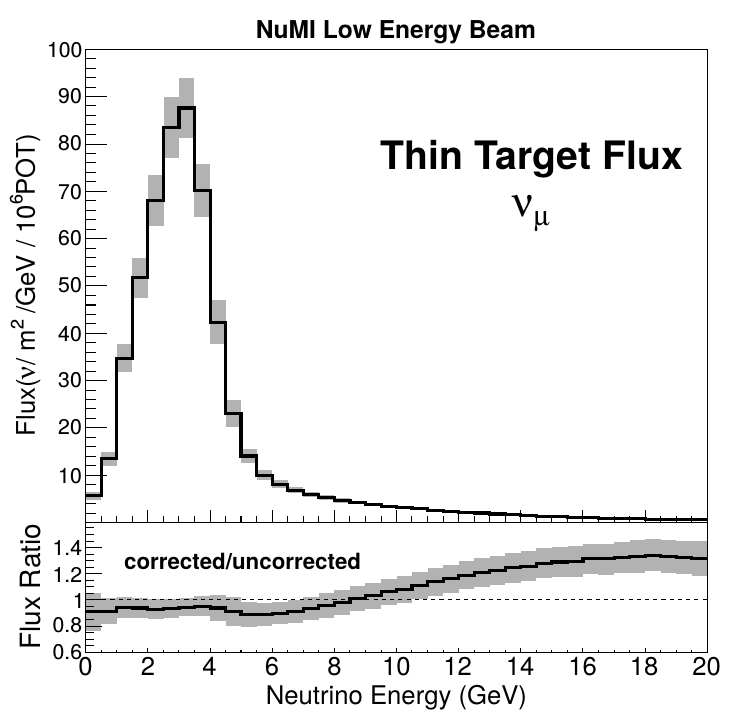
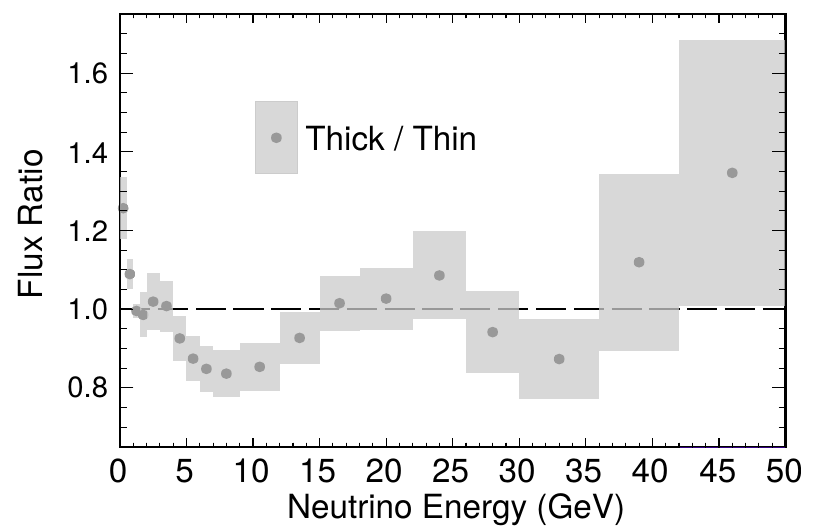
Whenever possible - "thick" target data is used
Uncertainties
Many-Universes method is used to propagate external data uncertainties to our flux
for each universe (u) data central value is shifted (respect to data uncertainties)
\[w_u \sim \prod_i w_{HP, u, i}\]
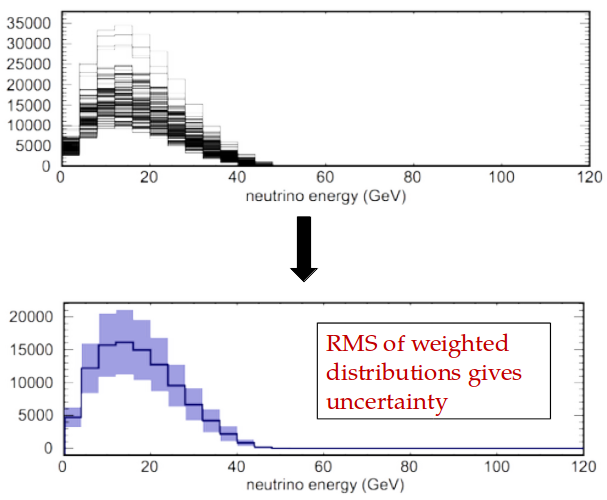
Flux history
Flux generations
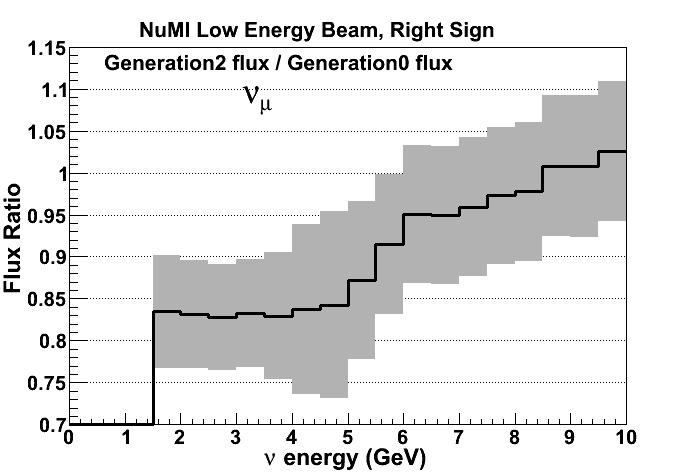
Generation 0 -> no MIPP data
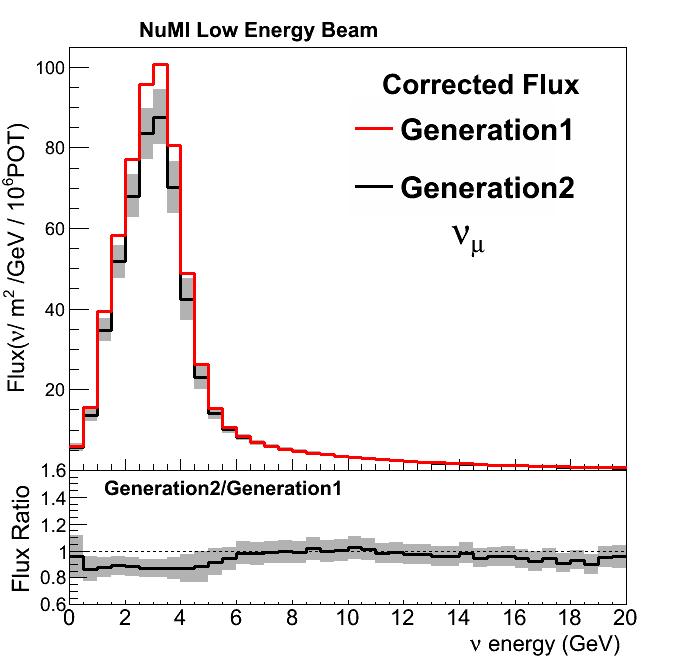
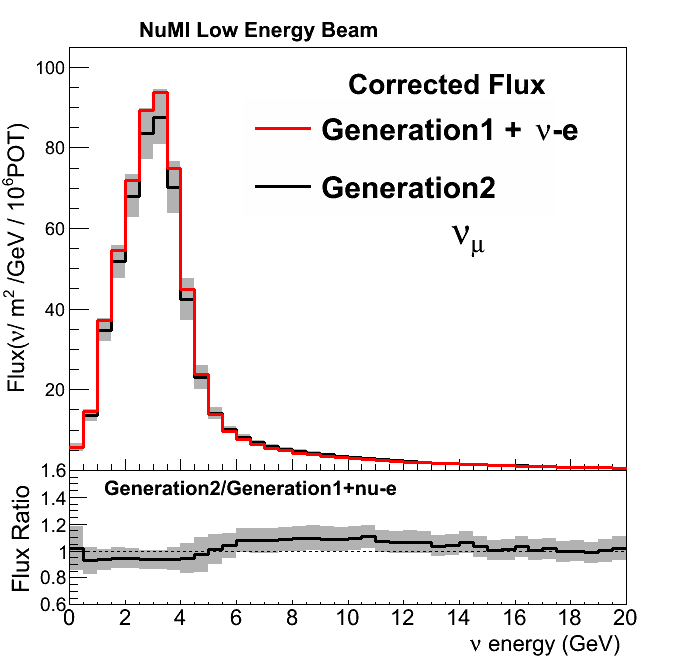
Generation 1 -> MIPP thin target data + other improvements
Generation 2 -> MIPP thick target data + other improvements
Flux vs publications
| Flux | Analysis | Reference |
|---|---|---|
| Generation 0 | \(\nu_\mu\) CCQE | PRL 111 (2013) 022502 |
| Generation 0 | \(\bar{\nu_\mu}\) CCQE | PRL 111 (2013) 022501 |
| Generation 1 | \(\nu_\mu\) muon + proton | PRD 91 (2015) 071301 |
| Generation 1 | \(\nu_\mu\) CC \(\pi^\pm\) | PRD 92 (2015) 092008 |
| Generation 1 | \(\bar{\nu_\mu}\) CC \(\pi^0\) | PLB 749 (2015) 130 |
| Generation 1 | Coherent \(\pi\) | PRL 113 (2014) 261802 |
| Generation 1 | CC target ratios | PRL 112 (2014) 231801 |
Generation 0 vs Generation 2 (thick off)
Generation 1 vs Generation 2 (thick off)
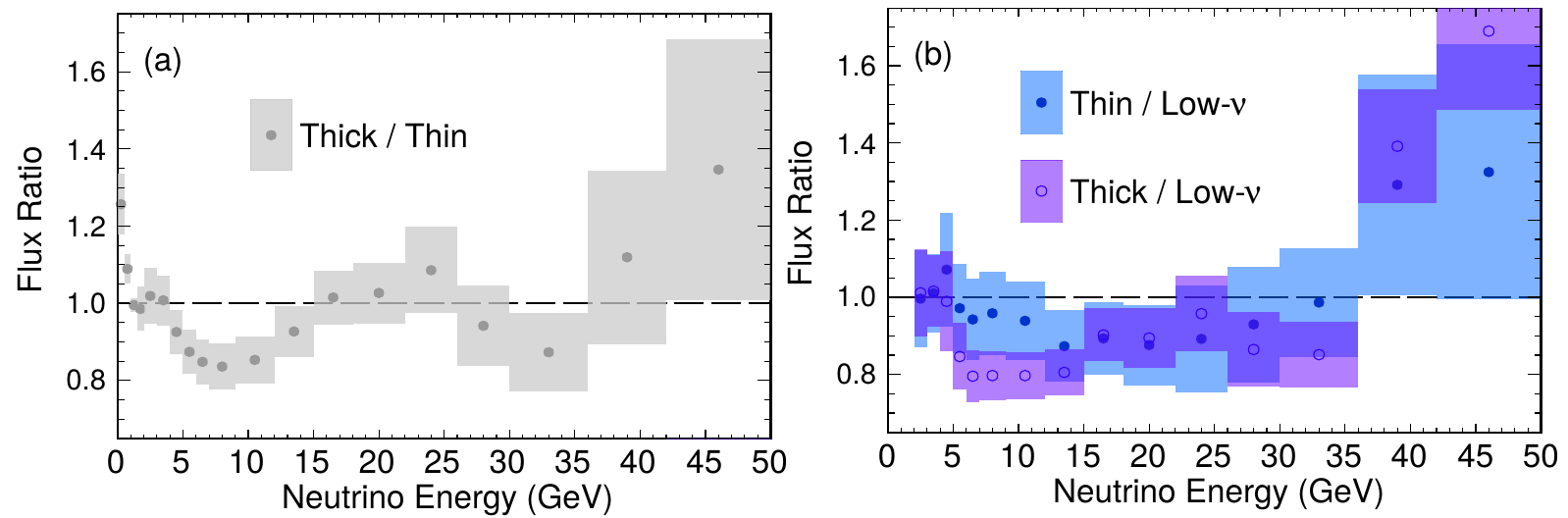
Generation 2 (thin vs thick)
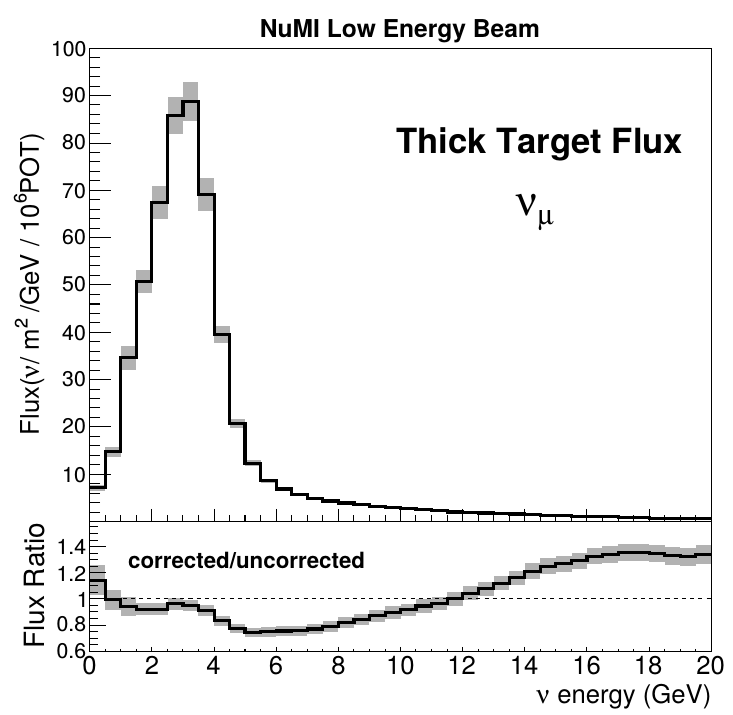
Generation 2: ratio
Flux constraints
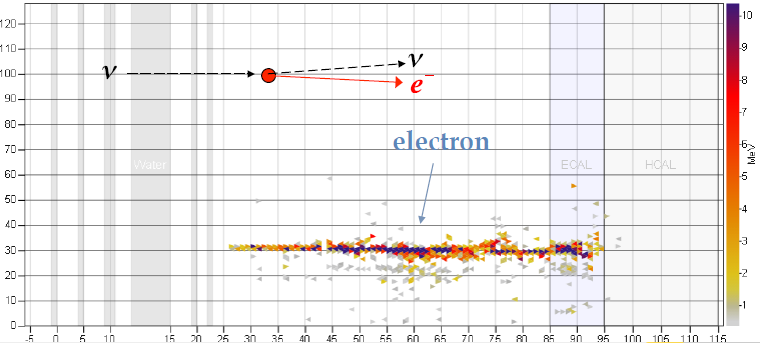
\(\nu e\) constraint
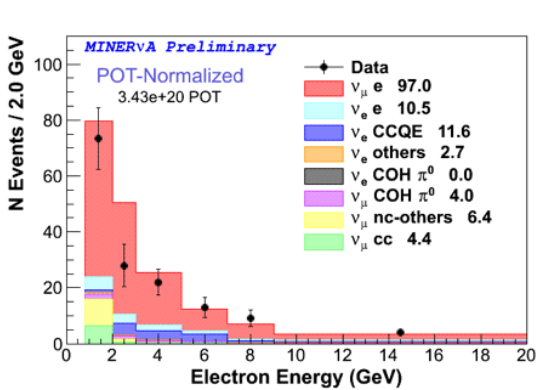
- Weighting up universes that agree better with data
- Experimental signature is a very forward single electron in the finale state
Generation 1 + \(\nu e\)

low-\(\nu\) method
\[\frac{d\sigma}{d\nu} = A + B\frac{\nu}{E} - \frac{C}{2}\frac{\nu^2}{E^2}\]
Differential cross-section can be expressed by the above formula
It is a constant for \(\frac{\nu}{E} \rightarrow 0\)
It can be used to constraint the flux prediction (with high-energy normalization taken from other measurements, like NOMAD)
low-\(\nu\) vs generation 2
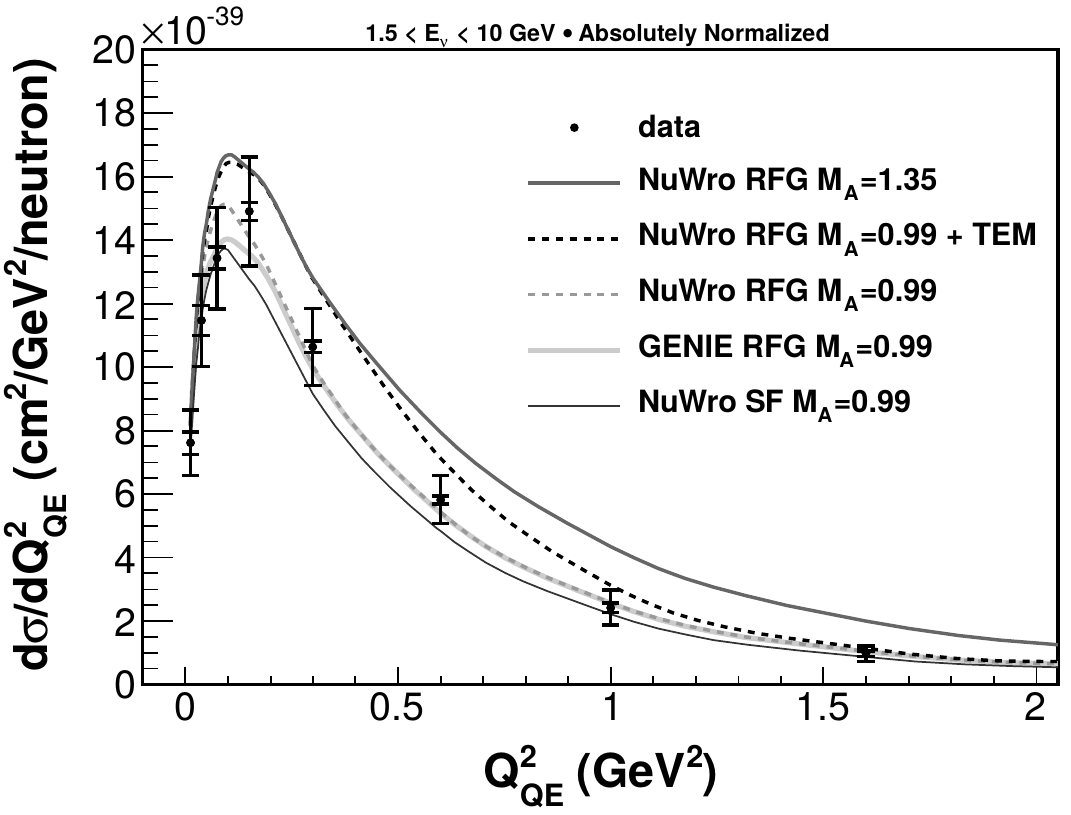
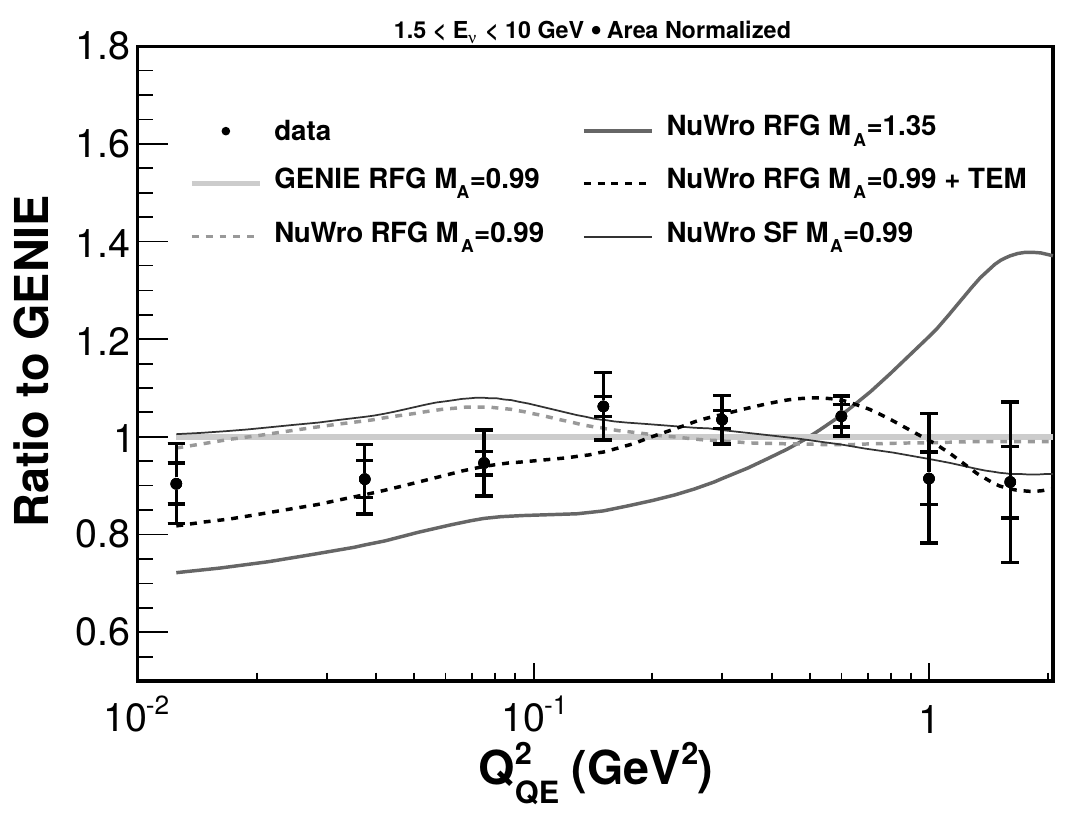
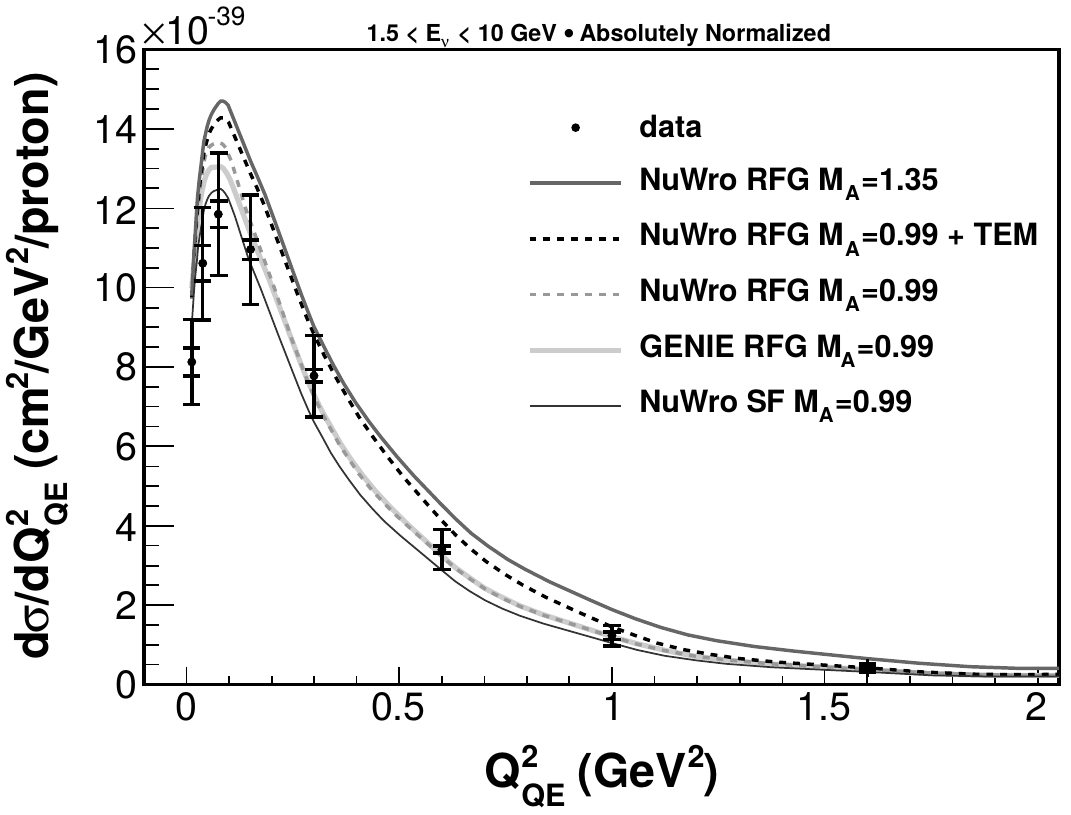
CCQE measurements
CCQE-"true" aka "1-track"
| Flux | Analysis | Reference |
|---|---|---|
| Generation 0 | \(\nu_\mu\) CCQE | PRL 111 (2013) 022502 |
| Generation 0 | \(\bar{\nu_\mu}\) CCQE | PRL 111 (2013) 022501 |
require only muon track
target -> scintillator (CH)
High-\(Q^2\) candidates
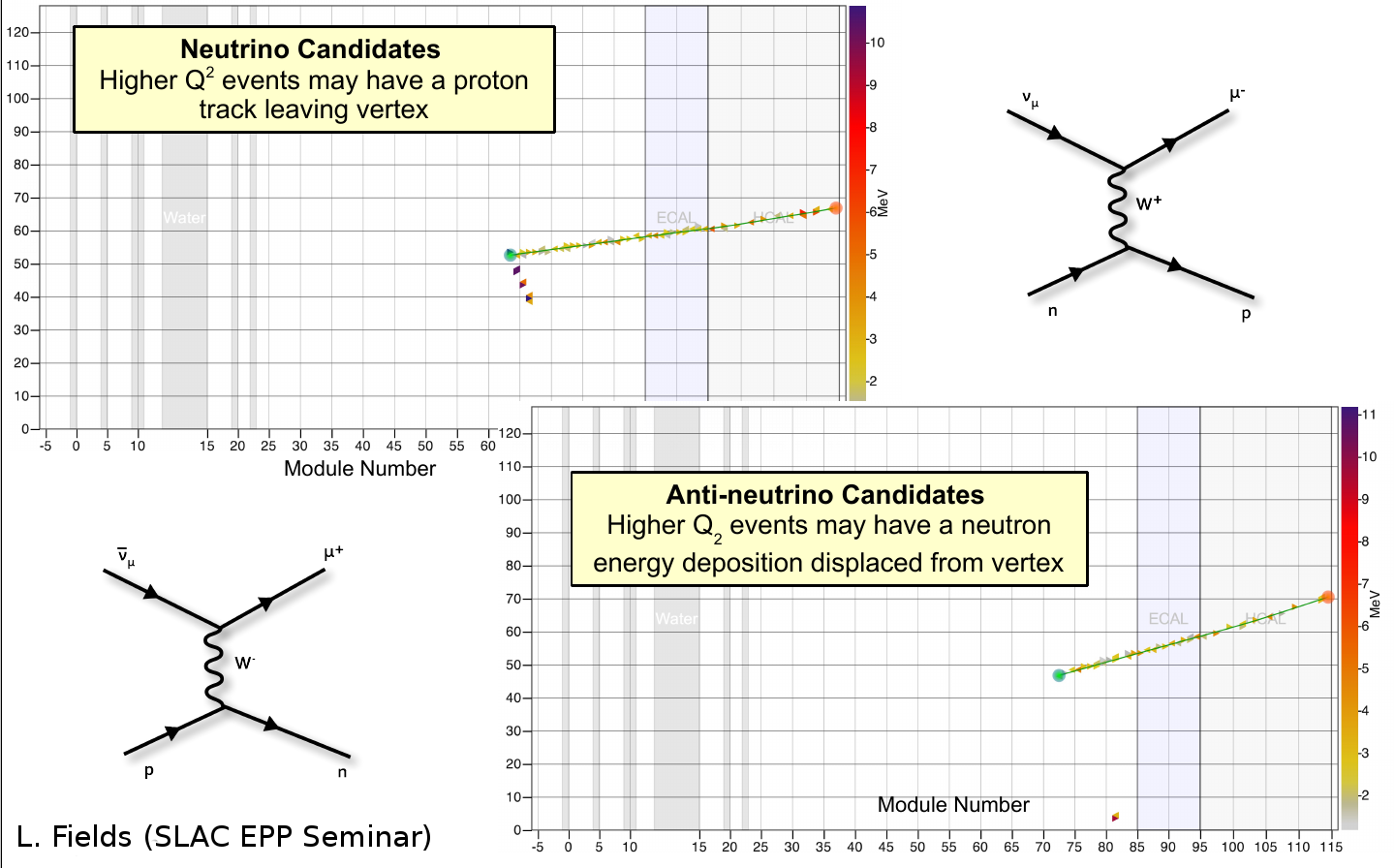
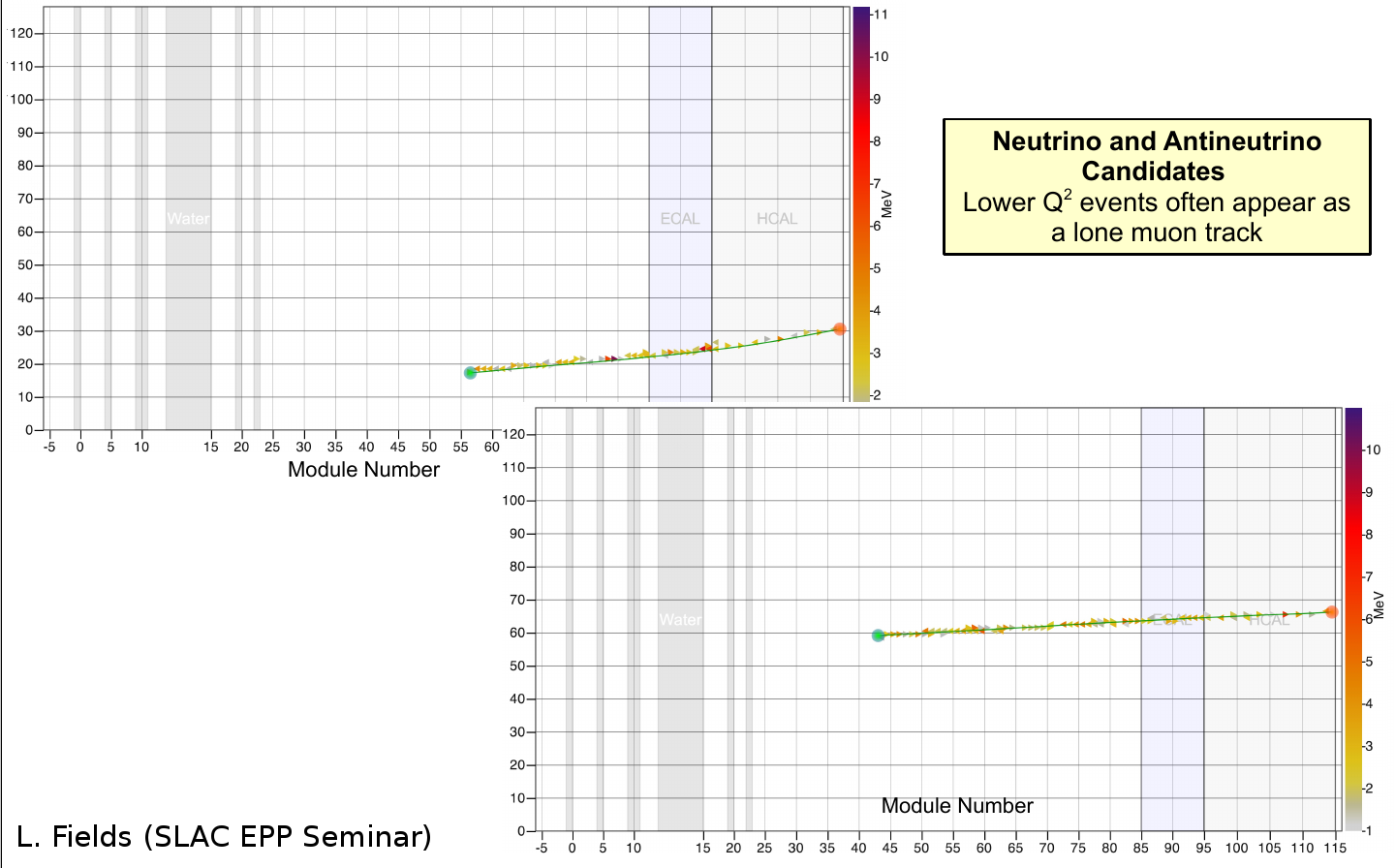
Low-\(Q^2\) candidates
Background
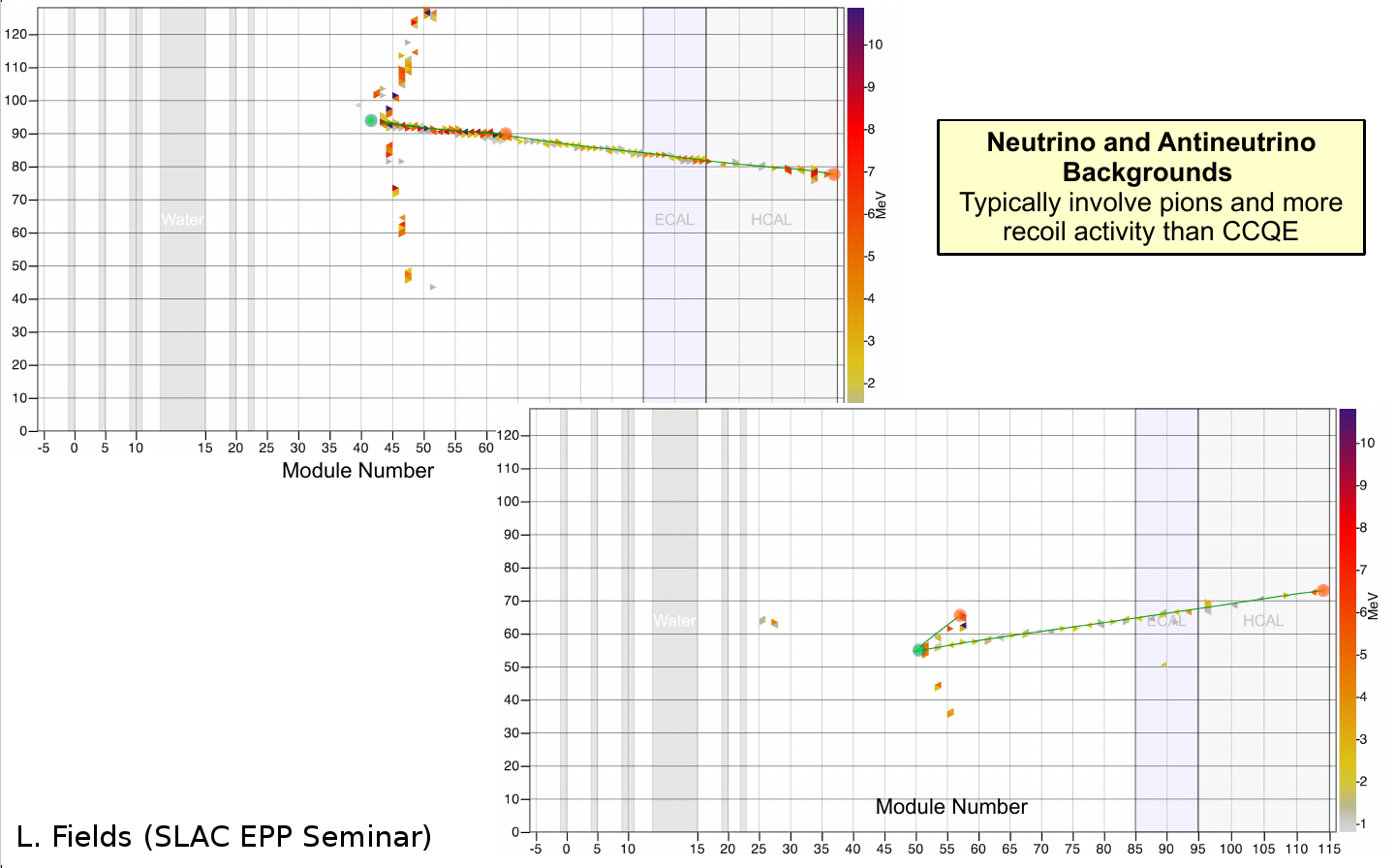
Background subtraction
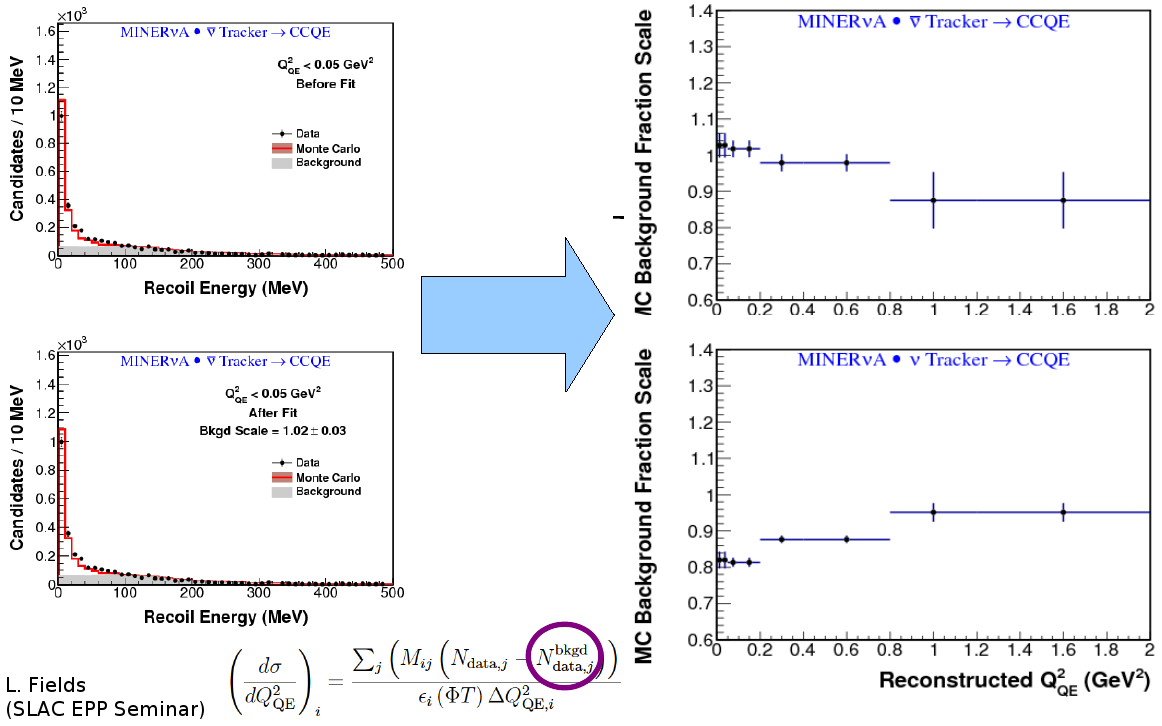
\(\nu_\mu\) CCQE
\(\bar\nu_\mu\) CCQE
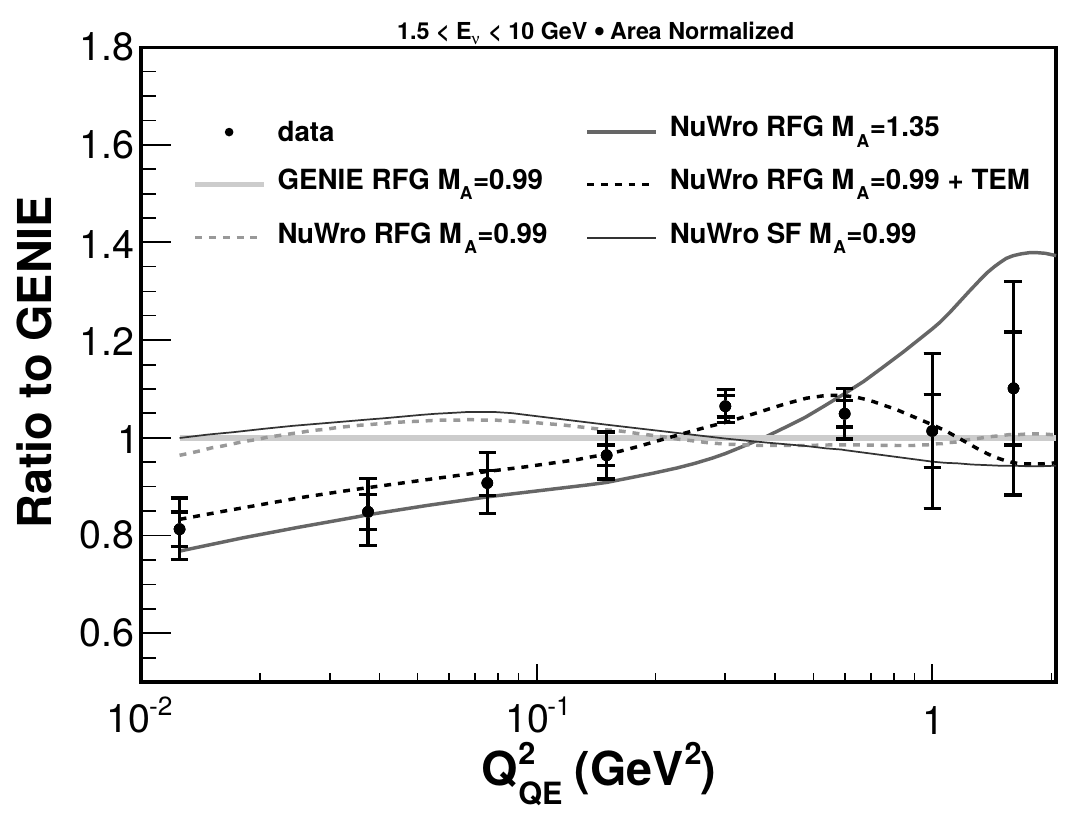
CCQE-"like" aka "muon+proton"
| Flux | Analysis | Reference |
|---|---|---|
| Generation 1 | \(\nu_\mu\) muon + proton | PRD (2015) 071301 |
CC \(\nu_\mu\) on \(CH\)
require a muon, at least one proton, and no pions in the final state
based on hadronic kinematics
proton kinetic energy > 110 MeV
\(\nu_\mu\) CCQE-like
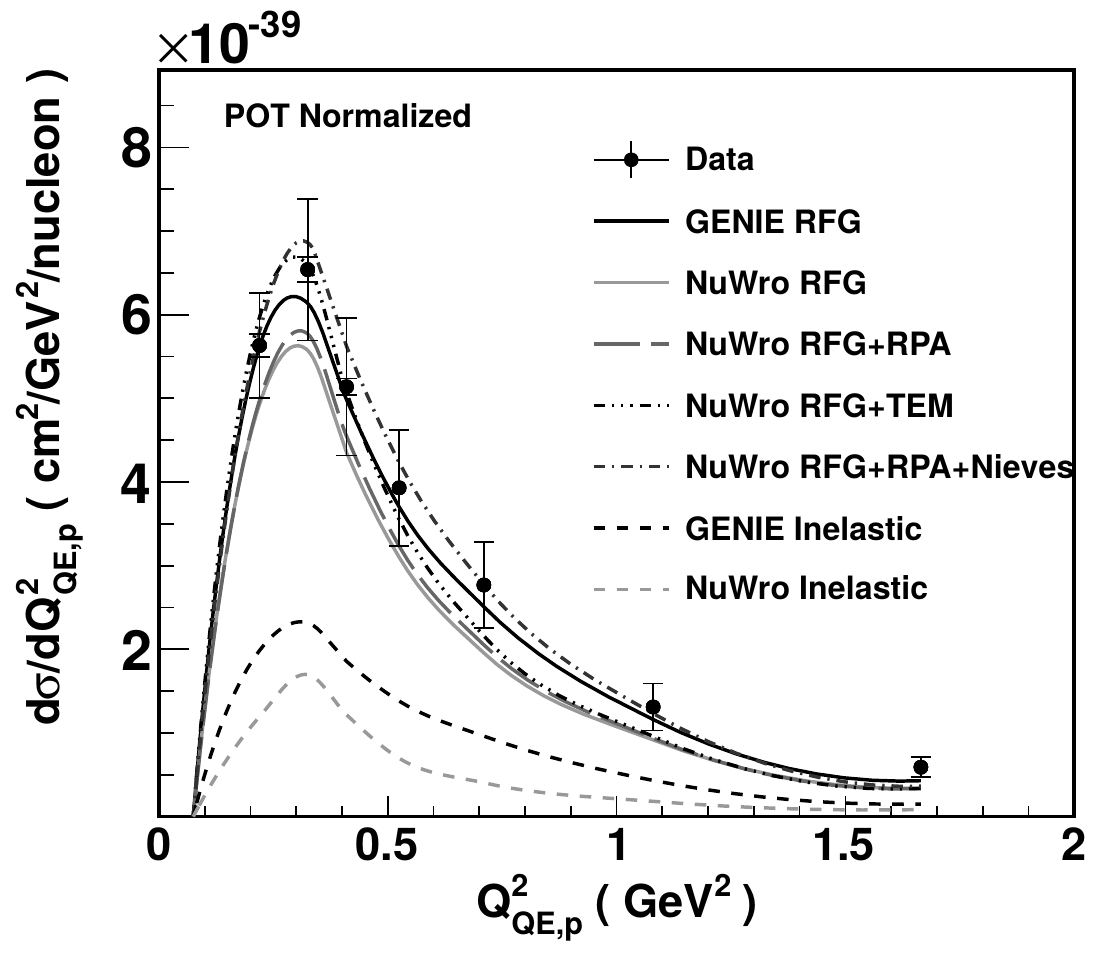
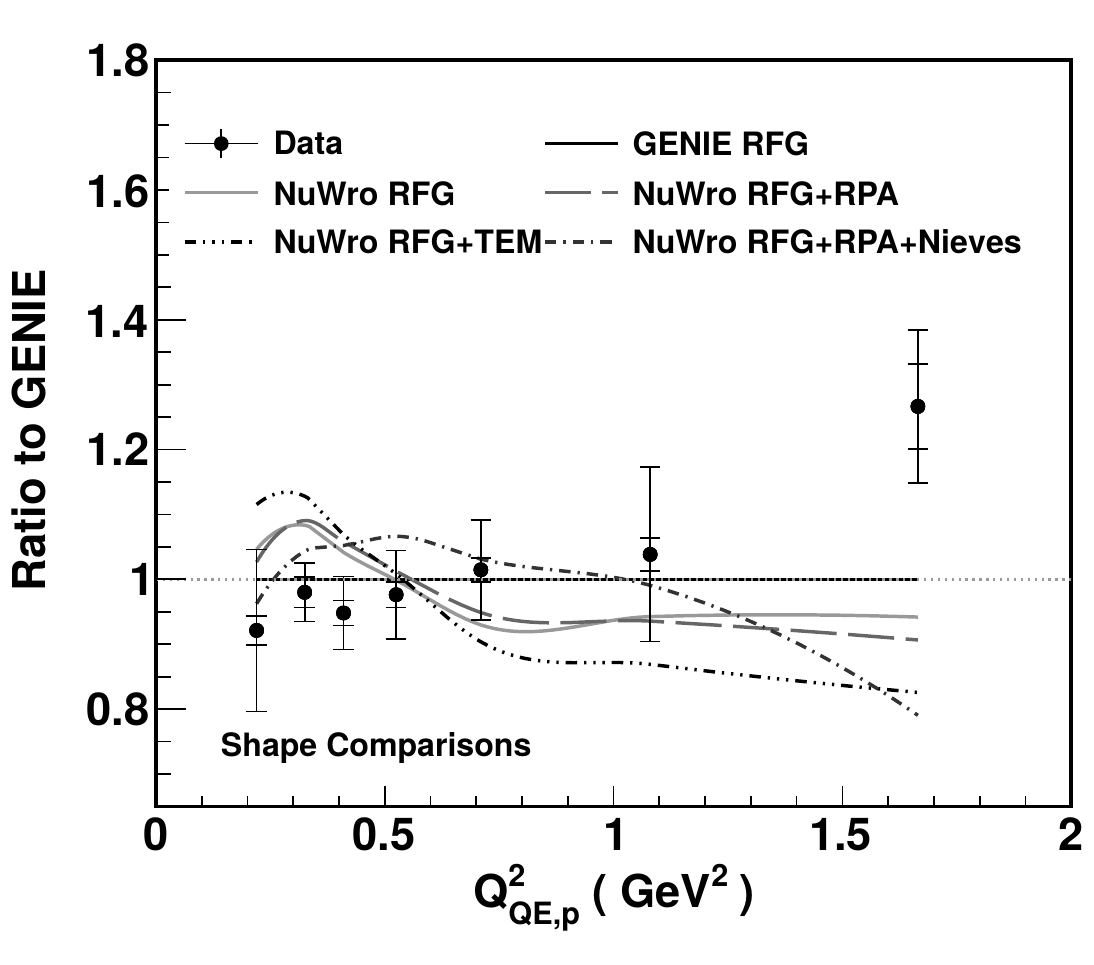
Pion production measurements
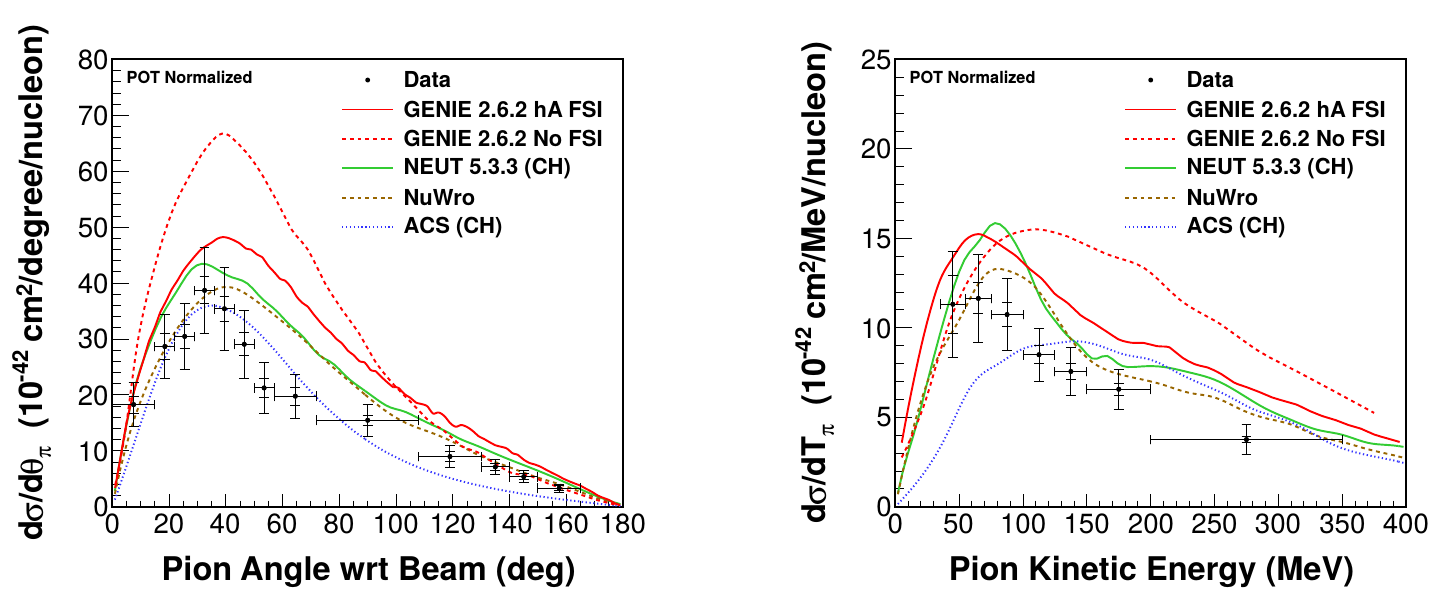
Charged pion production
CC \(1\pi^\pm\)
require a muon and exactly one charged pion
\(W < 1.4\) GeV
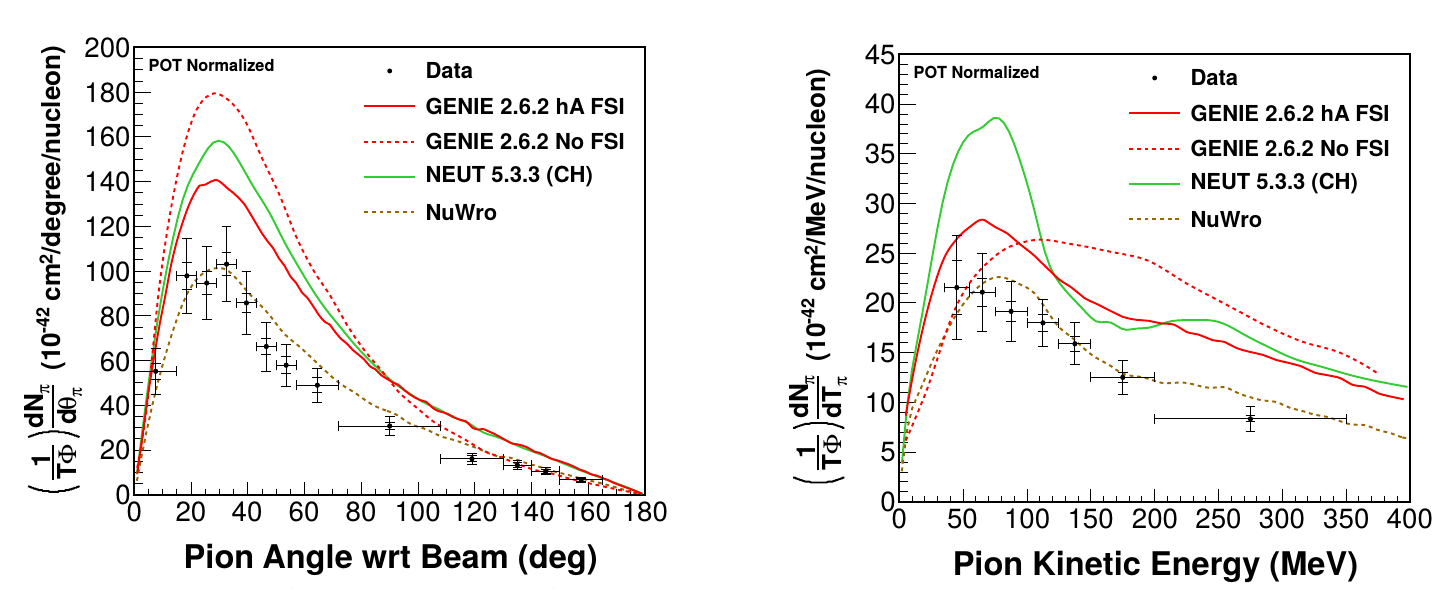
CC \(N\pi^\pm\)
require a muon and at least one charged pion
\(W < 1.8\) GeV
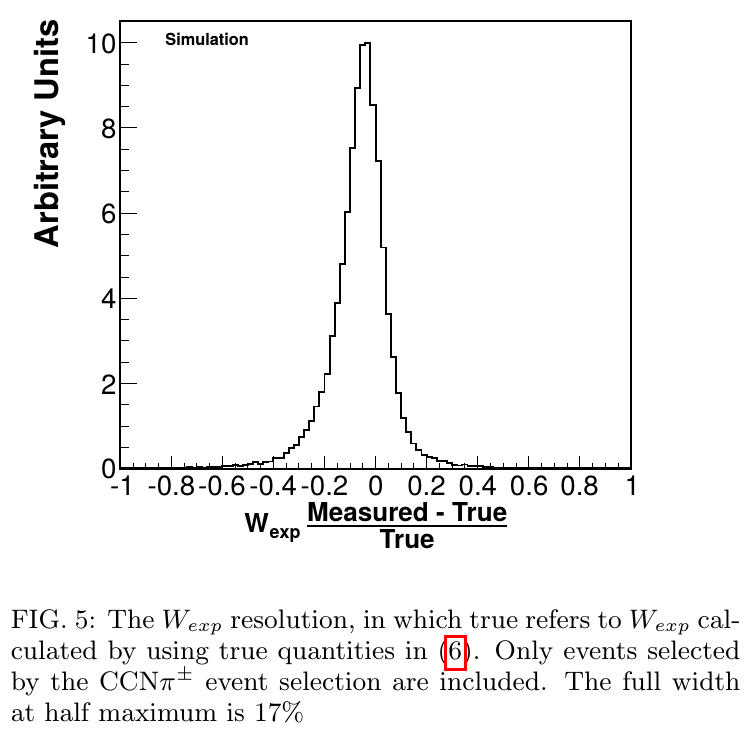
Invariant mass
\[E_\nu = E_\mu + E_{recoil}\] \[Q^2 = 2E_\nu(E_\mu - |\vec p_\mu|\cos\theta_\mu) - m_\mu^2\] \[W_{exp}^2 = M_p^2 - Q^2 + 2M_pE_{recoil}\]
- \(E_{recoil}\) is measured colorimetrically
Backrounds vs invariant mass
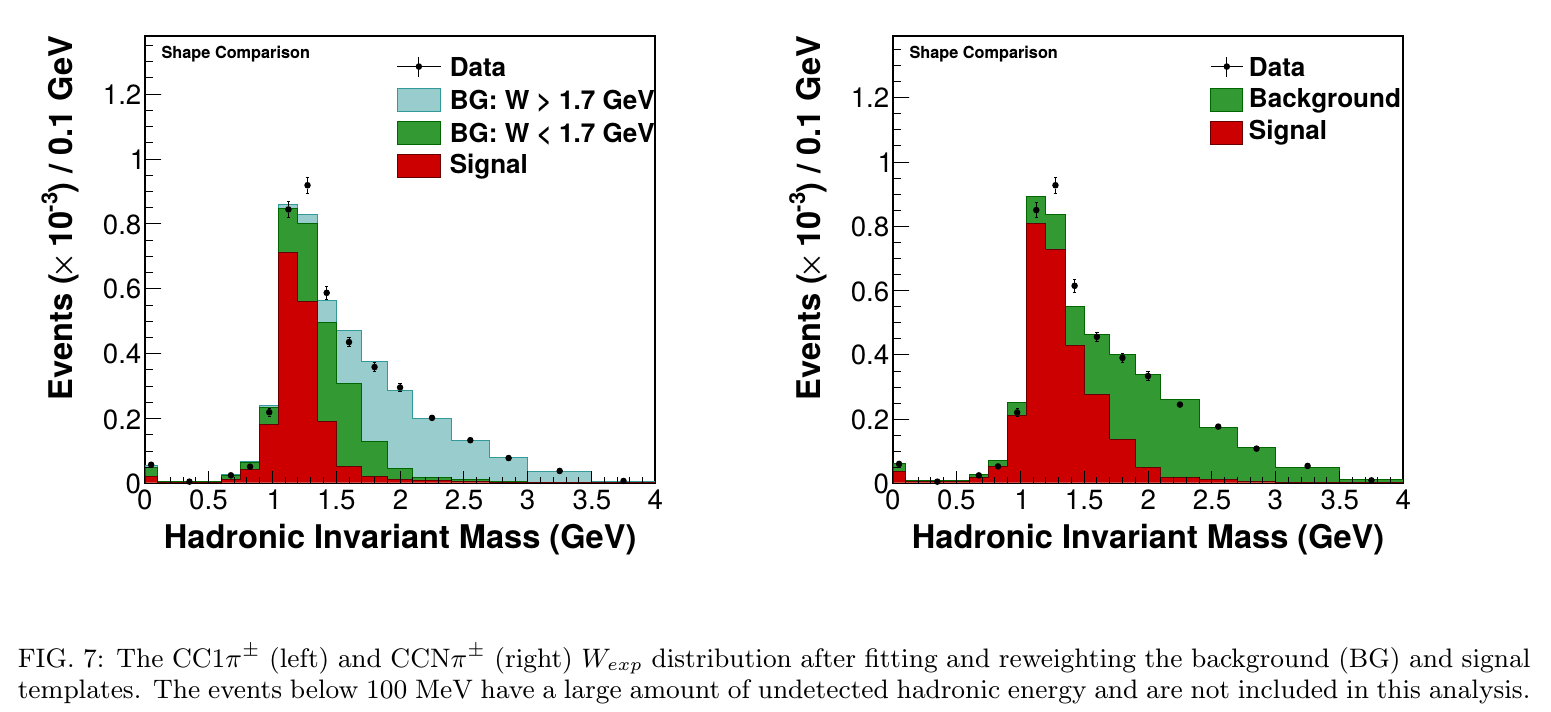
CC \(1\pi^\pm\)
CC \(N\pi^\pm\)
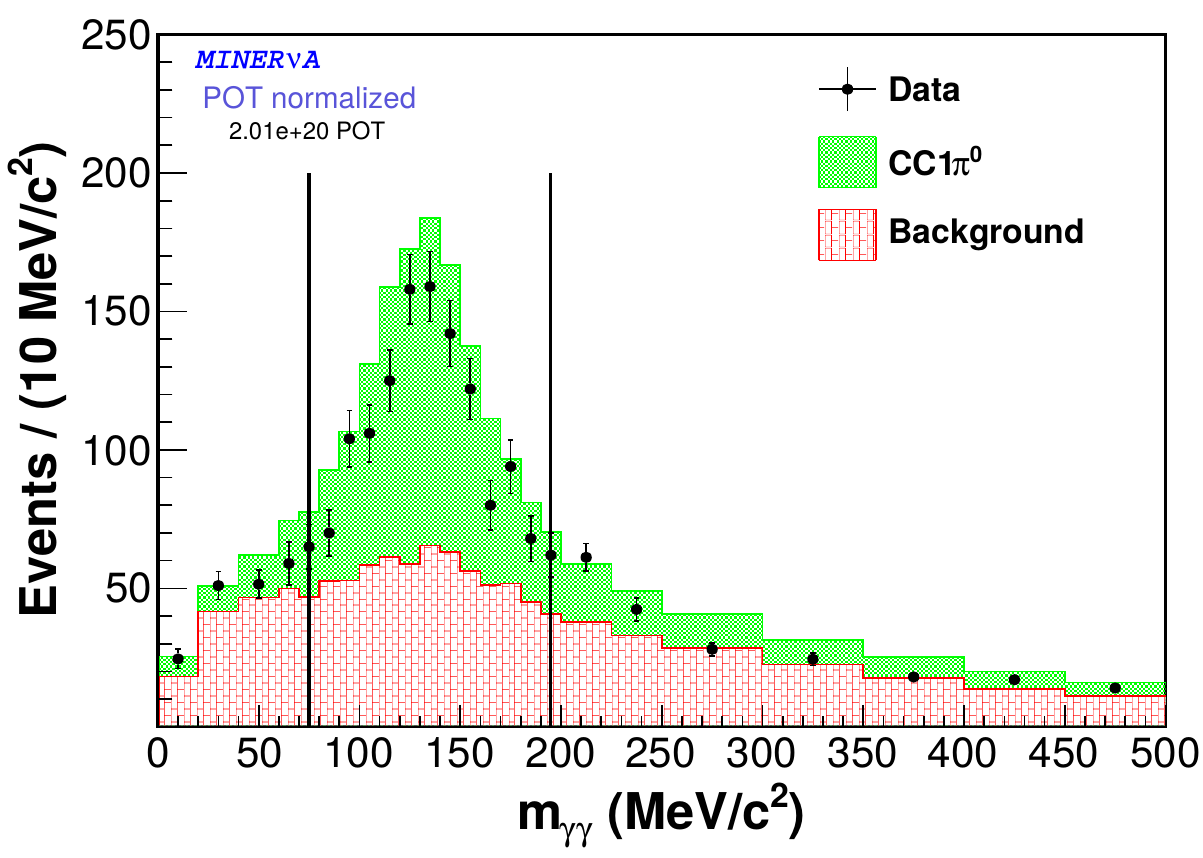
\(\bar\nu_\mu\) CC \(1\pi^0\)
- require a muon and a single neutral pion (visible as two photons)
- about 70% of background - multipion events \(\pi^0 + \pi^\pm\)
- \(pi^\pm\) is not tracked
- \(\pi^-\rightarrow\pi^0\)
- the rest of the background is mostly due to energy deposit by \(\pi^-\) and neutrons misidentified as photons
Invariant mass of \(\gamma\gamma\)
The \(\gamma\gamma\) invariant mass is reconstructed from the photon energies (\(E_1\), \(E_2\)):
\[m_{\gamma\gamma}^2 = 2E_1E_2(1 - \cos\theta_{\gamma\gamma})\]
Differential cross sections
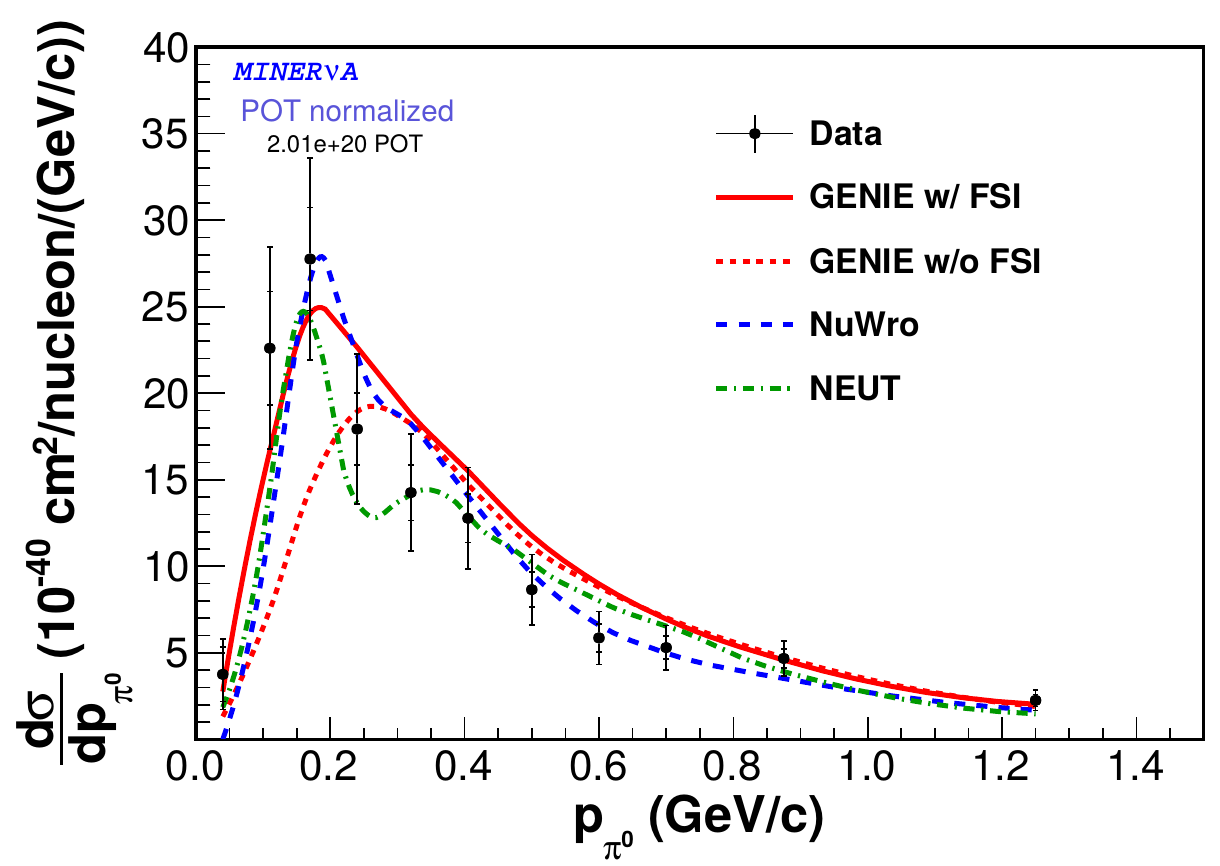
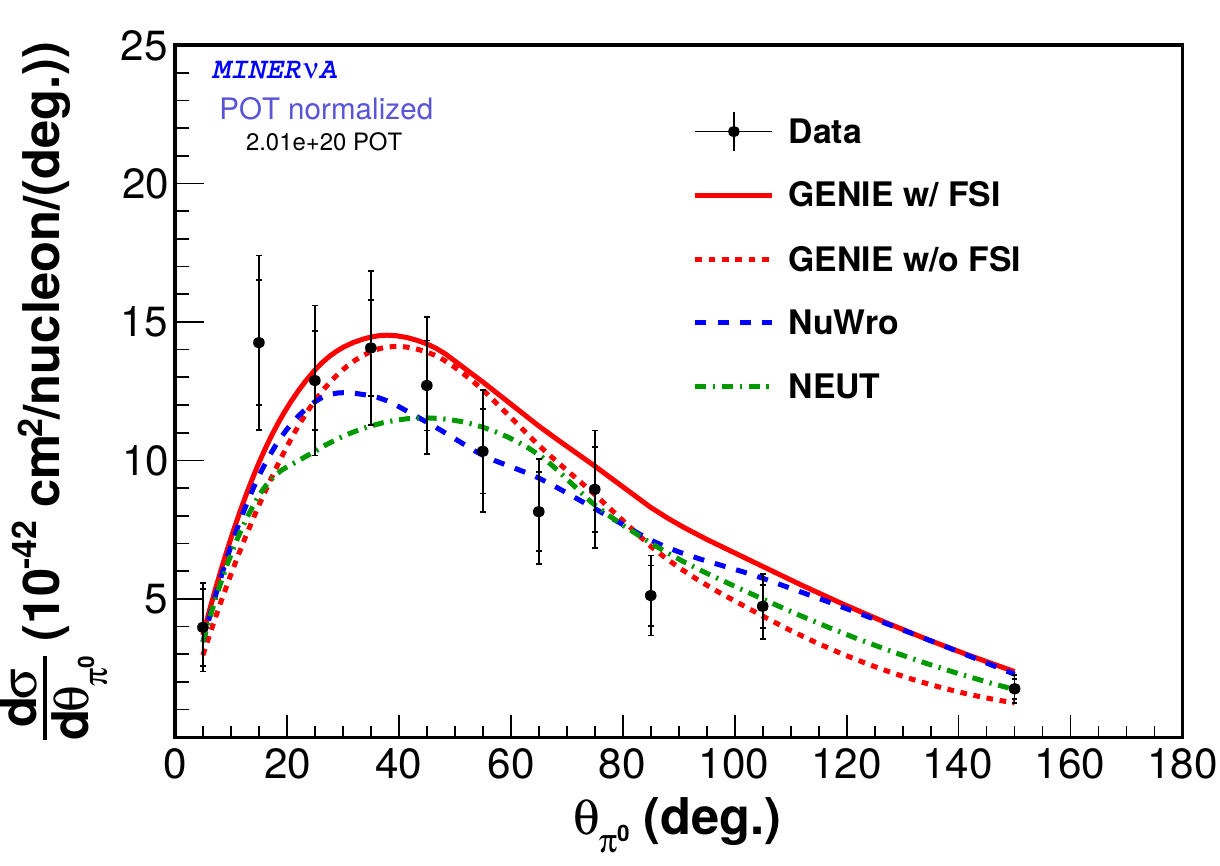
Coherent pion production
- require two final state particles: \(\mu^\pm\) and \(\pi^\mp\) and no extra visible recoil
Background
Low energy transfer requirement
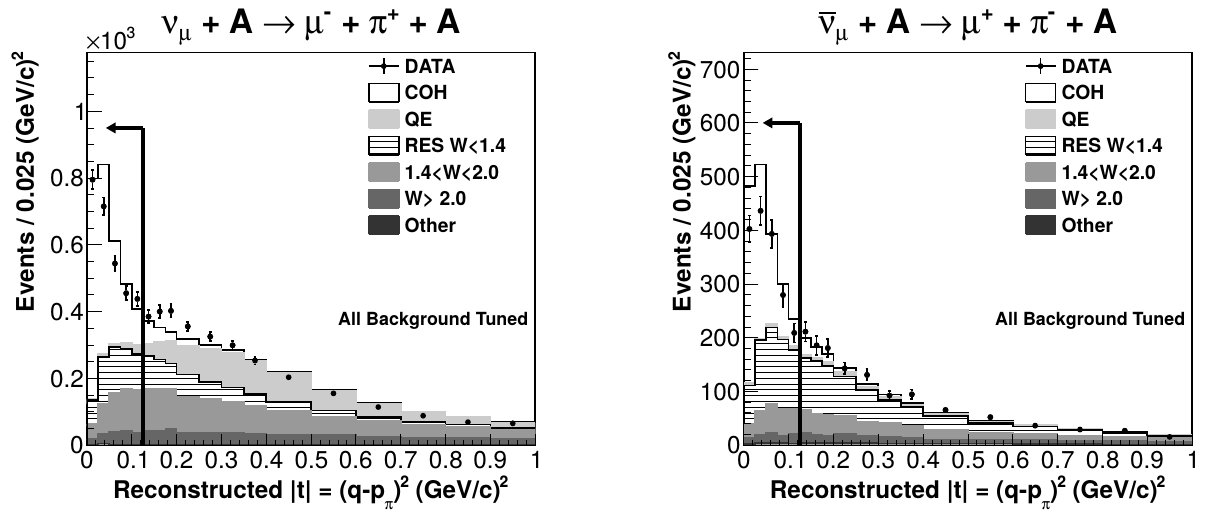
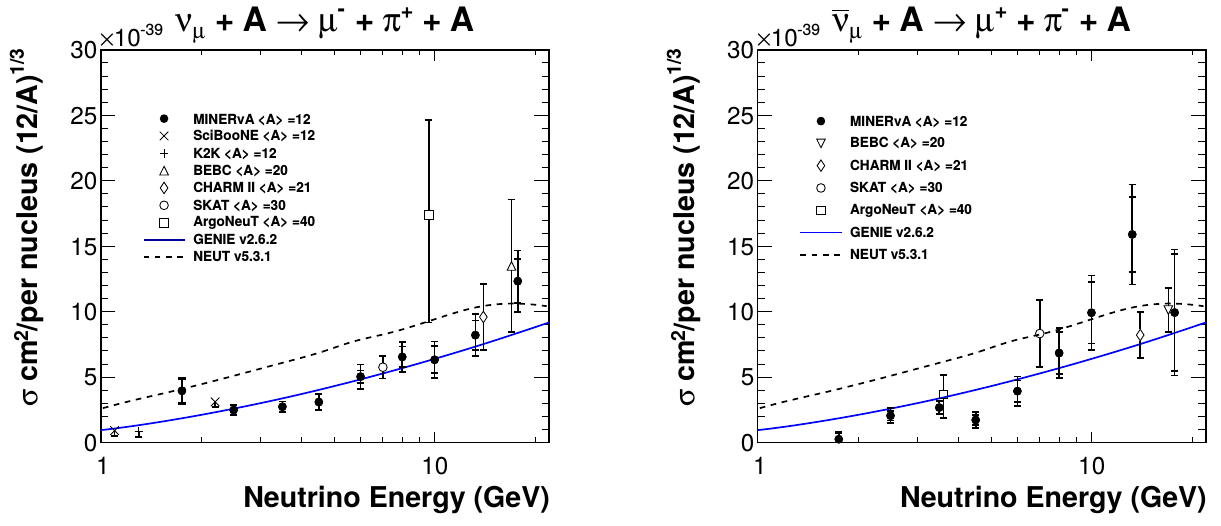
Total cross section
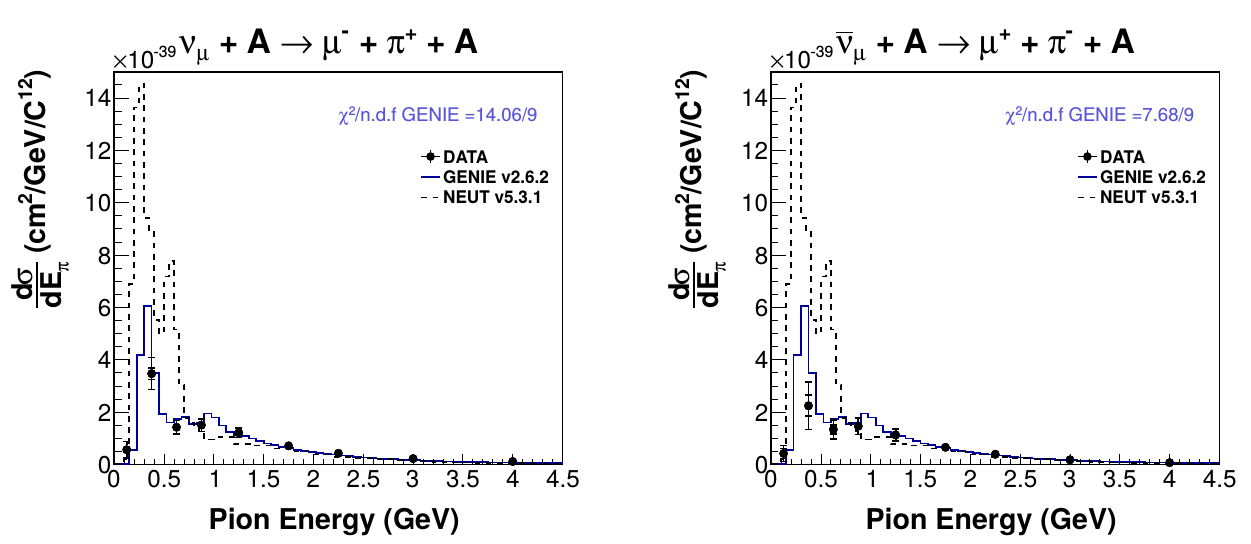
Differential cross section (energy)
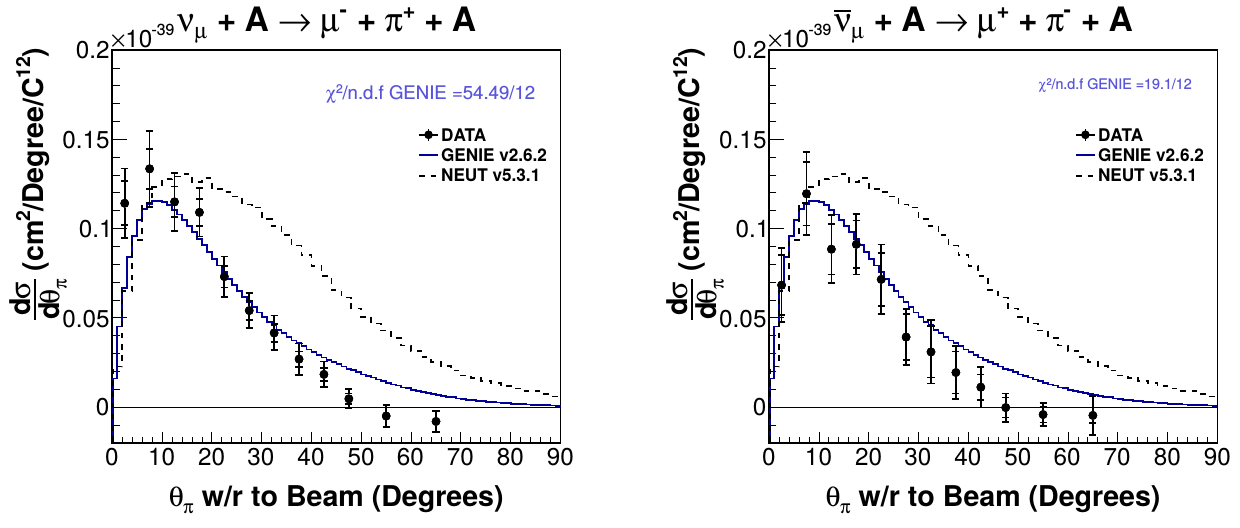
Differential cross section (angle)
Other measurements highlights
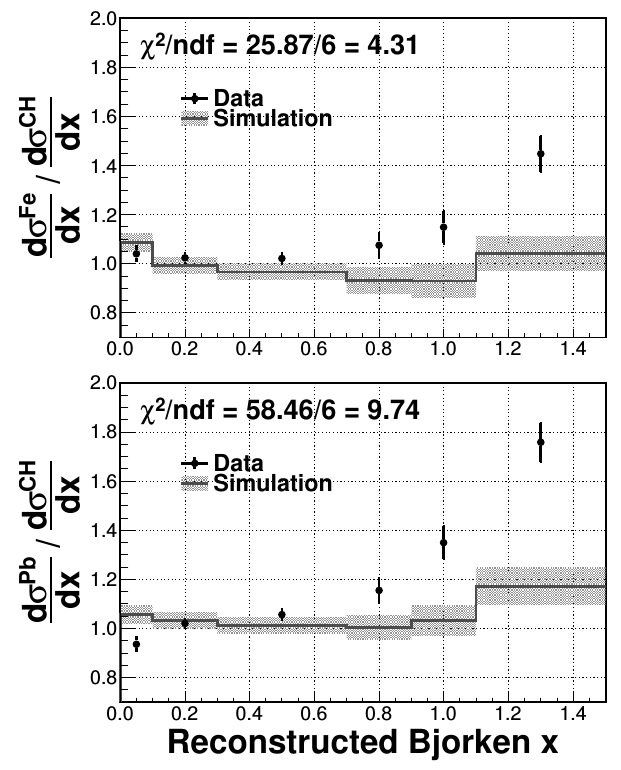
Inclusive \(\nu_\mu\) CC ratios
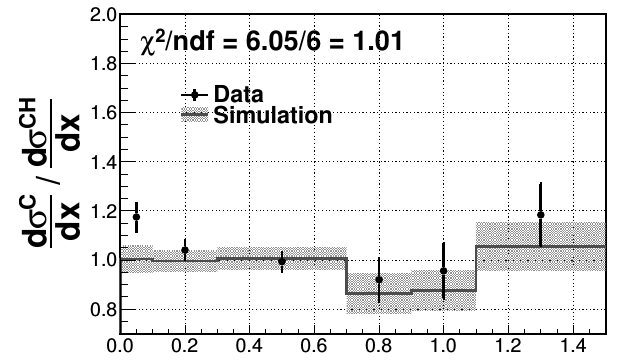
shadowing at low \(x\)
no MEC in simulations (high \(x\) dominated by QE)
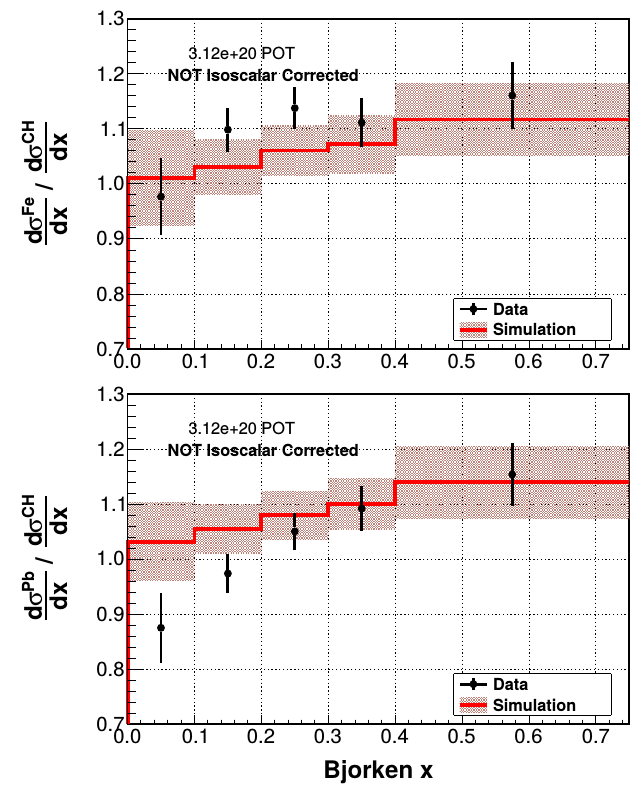
DIS \(\nu_\mu\) CC ratios
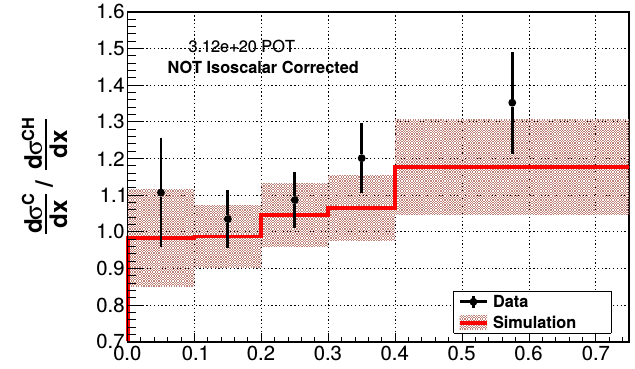
\(W > 2\) GeV and \(Q^2 > 1\) GeV\(^2\)
\(E_\nu\) up to 50 GeV
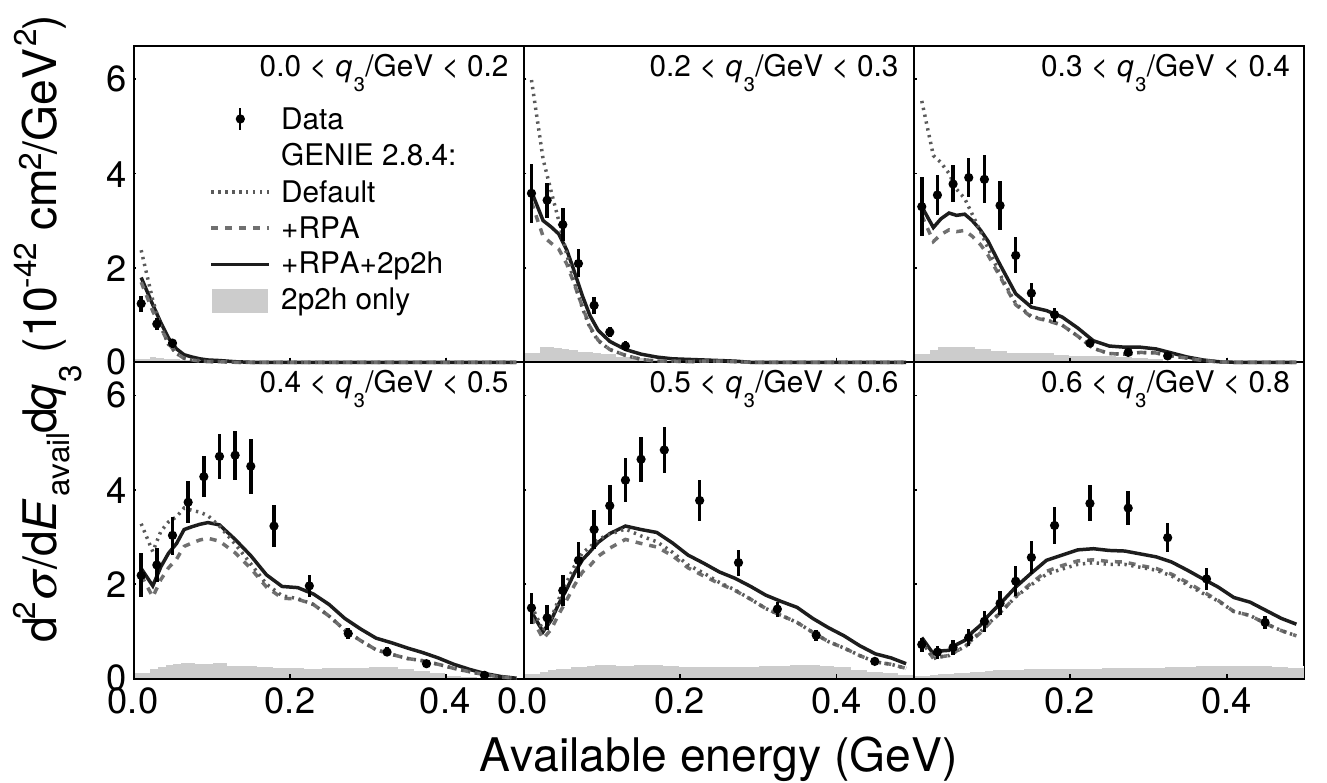
Available energy vs momentum transfer
- \(E_{avail}\) - sum of proton and charged pion kinetic energy and neutral pion, electron, and photon total energy
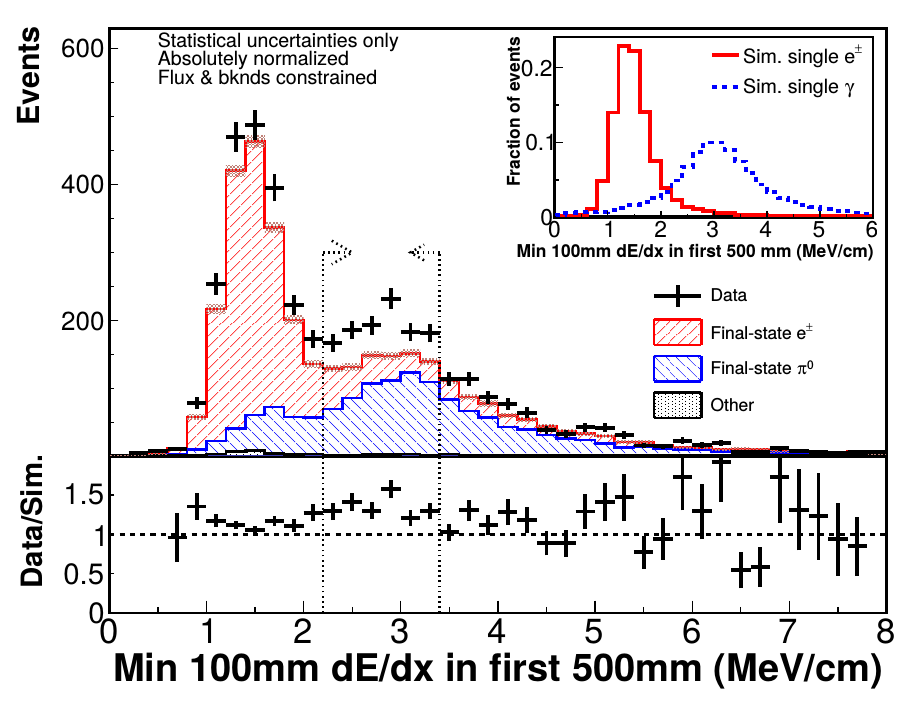
NC diffractive \(\pi^0\) production
- The most plausible source of the excess seen in the data is diffractive NC \(\pi^0\) production from hydrogen in the scintillator target of MINERvA.
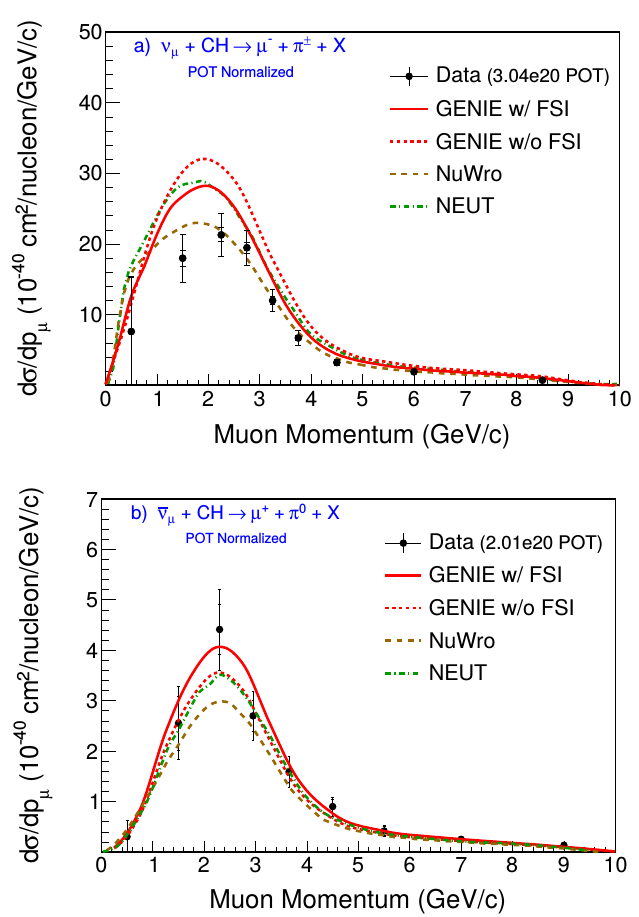
CC pion production (muon variables)
\(\nu\)-CC(\(\pi^+\)) and \(\bar\nu\)-CC(\(\pi^0\))
total cross section
differential cross sections:
- muon momentum
- muon angle
- \(Q^2\)
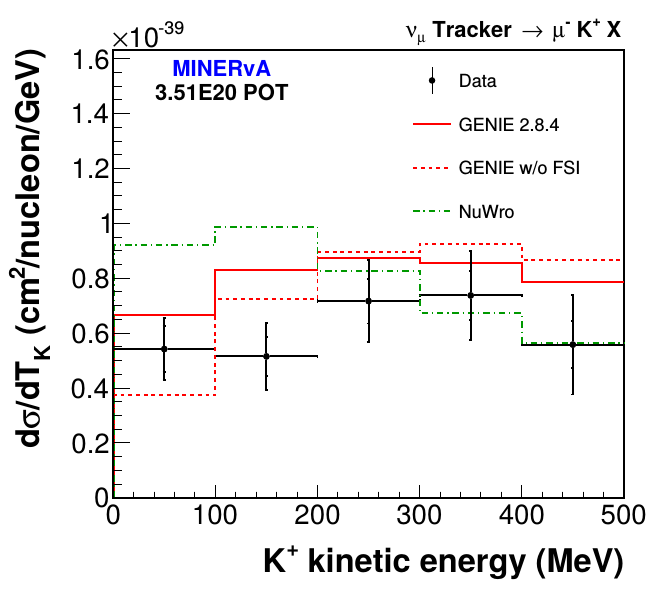
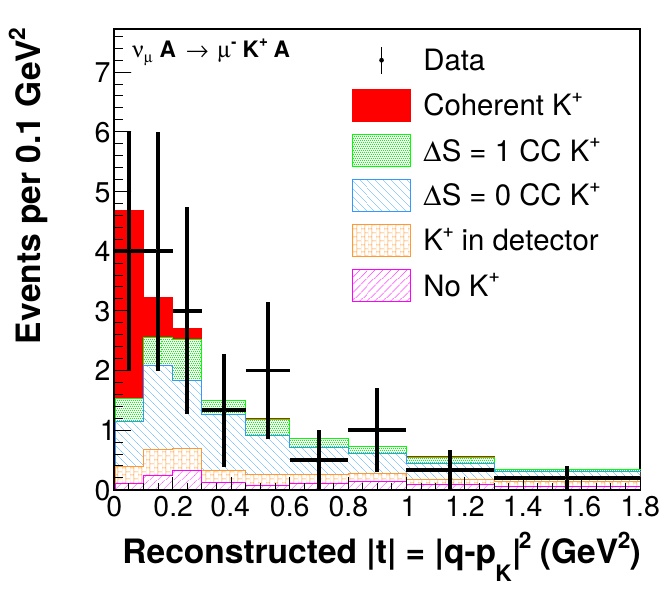
Kaon production
Summary
MINERvA offers an unique opportunity to measure neutrino cross section on different nuclear targets
There is still a lot of collected data to study (e.g. in nuclear target region)
Medium energy data will allow to study more precisely DIS (and transition region?)